James Humann
Risk-aware Resource Allocation for Multiple UAVs-UGVs Recharging Rendezvous
Sep 13, 2022

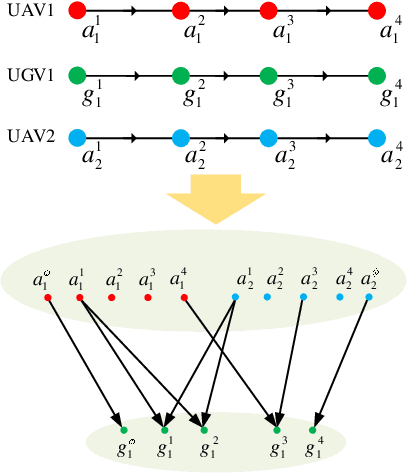
Abstract:We study a resource allocation problem for the cooperative aerial-ground vehicle routing application, in which multiple Unmanned Aerial Vehicles (UAVs) with limited battery capacity and multiple Unmanned Ground Vehicles (UGVs) that can also act as a mobile recharging stations need to jointly accomplish a mission such as persistently monitoring a set of points. Due to the limited battery capacity of the UAVs, they sometimes have to deviate from their task to rendezvous with the UGVs and get recharged. Each UGV can serve a limited number of UAVs at a time. In contrast to prior work on deterministic multi-robot scheduling, we consider the challenge imposed by the stochasticity of the energy consumption of the UAV. We are interested in finding the optimal recharging schedule of the UAVs such that the travel cost is minimized and the probability that no UAV runs out of charge within the planning horizon is greater than a user-defined tolerance. We formulate this problem ({Risk-aware Recharging Rendezvous Problem (RRRP))} as an Integer Linear Program (ILP), in which the matching constraint captures the resource availability constraints and the knapsack constraint captures the success probability constraints. We propose a bicriteria approximation algorithm to solve RRRP. We demonstrate the effectiveness of our formulation and algorithm in the context of one persistent monitoring mission.
Risk-aware UAV-UGV Rendezvous with Chance-Constrained Markov Decision Process
Apr 10, 2022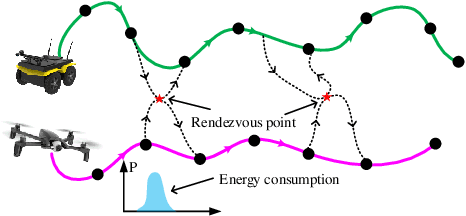
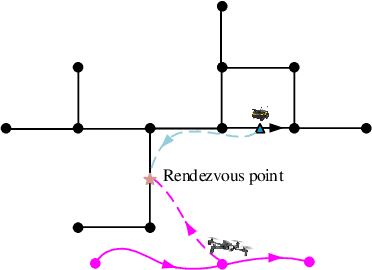
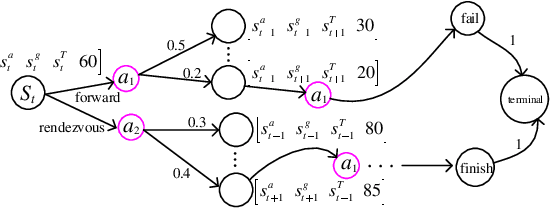
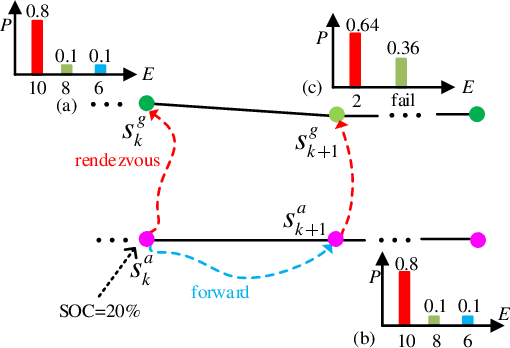
Abstract:We study a chance-constrained variant of the cooperative aerial-ground vehicle routing problem, in which an Unmanned Aerial Vehicle (UAV) with limited battery capacity and an Unmanned Ground Vehicle (UGV) that can also act as a mobile recharging station need to jointly accomplish a mission such as monitoring a set of points. Due to the limited battery capacity of the UAV, two vehicles sometimes have to deviate from their task to rendezvous and recharge the UAV\@. Unlike prior work that has focused on the deterministic case, we address the challenge of stochastic energy consumption of the UAV\@. We are interested in finding the optimal policy that decides when and where to rendezvous such that the expected travel time of the UAV is minimized and the probability of running out of charge is less than a user-defined tolerance. We formulate this problem as a Chance Constrained Markov Decision Process (CCMDP). To the best knowledge of the authors, this is the first CMDP-based formulation for the UAV-UGV routing problems under power consumption uncertainty. We adopt a Linear Programming (LP) based approach to solve the problem optimally. We demonstrate the effectiveness of our formulation in the context of an Intelligence Surveillance and Reconnaissance (ISR) mission.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge