Online Hyperparameter Meta-Learning with Hypergradient Distillation

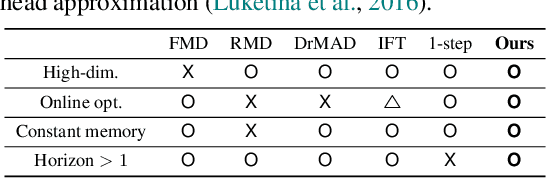
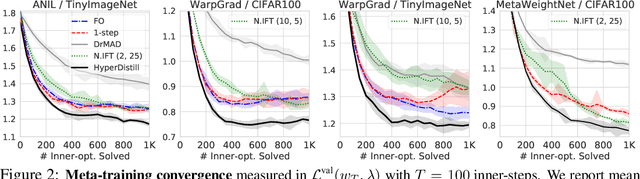
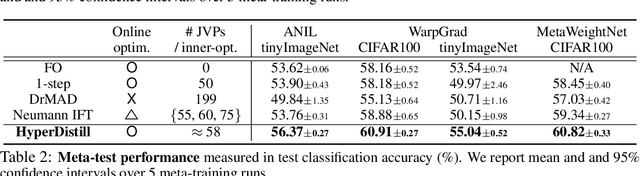
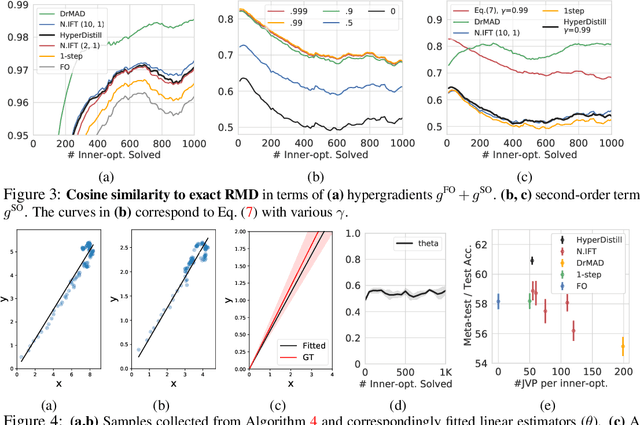
Many gradient-based meta-learning methods assume a set of parameters that do not participate in inner-optimization, which can be considered as hyperparameters. Although such hyperparameters can be optimized using the existing gradient-based hyperparameter optimization (HO) methods, they suffer from the following issues. Unrolled differentiation methods do not scale well to high-dimensional hyperparameters or horizon length, Implicit Function Theorem (IFT) based methods are restrictive for online optimization, and short horizon approximations suffer from short horizon bias. In this work, we propose a novel HO method that can overcome these limitations, by approximating the second-order term with knowledge distillation. Specifically, we parameterize a single Jacobian-vector product (JVP) for each HO step and minimize the distance from the true second-order term. Our method allows online optimization and also is scalable to the hyperparameter dimension and the horizon length. We demonstrate the effectiveness of our method on two different meta-learning methods and three benchmark datasets.

Large-Scale Meta-Learning with Continual Trajectory Shifting

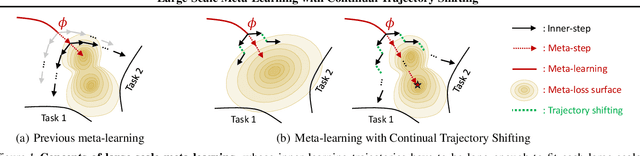
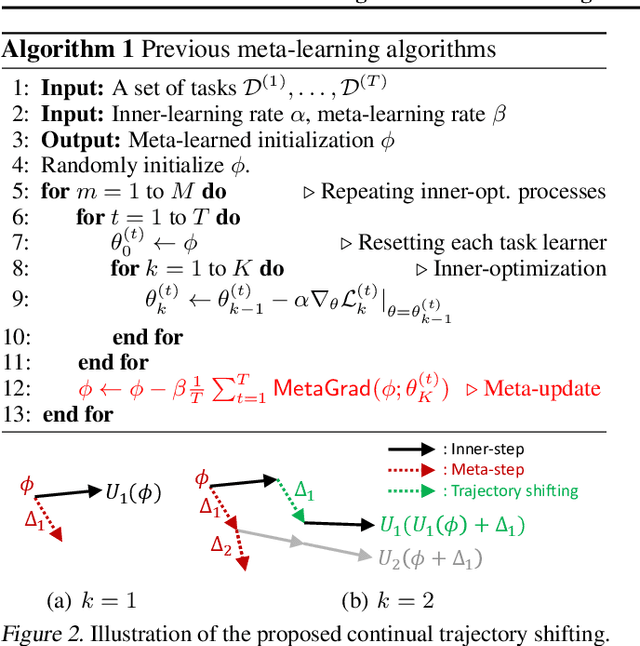
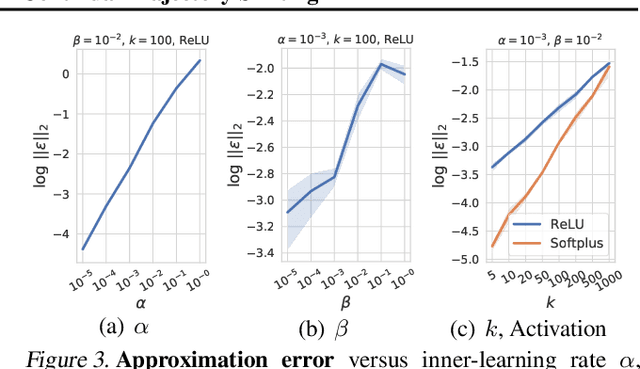
Meta-learning of shared initialization parameters has shown to be highly effective in solving few-shot learning tasks. However, extending the framework to many-shot scenarios, which may further enhance its practicality, has been relatively overlooked due to the technical difficulties of meta-learning over long chains of inner-gradient steps. In this paper, we first show that allowing the meta-learners to take a larger number of inner gradient steps better captures the structure of heterogeneous and large-scale task distributions, thus results in obtaining better initialization points. Further, in order to increase the frequency of meta-updates even with the excessively long inner-optimization trajectories, we propose to estimate the required shift of the task-specific parameters with respect to the change of the initialization parameters. By doing so, we can arbitrarily increase the frequency of meta-updates and thus greatly improve the meta-level convergence as well as the quality of the learned initializations. We validate our method on a heterogeneous set of large-scale tasks and show that the algorithm largely outperforms the previous first-order meta-learning methods in terms of both generalization performance and convergence, as well as multi-task learning and fine-tuning baselines.

MetaPerturb: Transferable Regularizer for Heterogeneous Tasks and Architectures

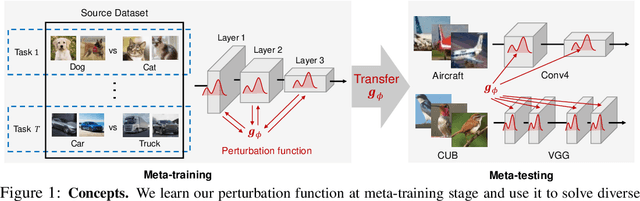
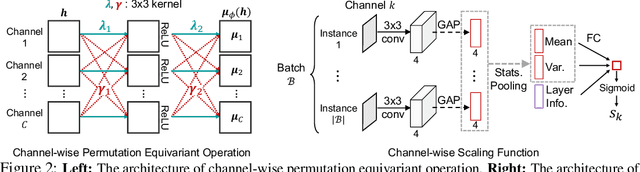
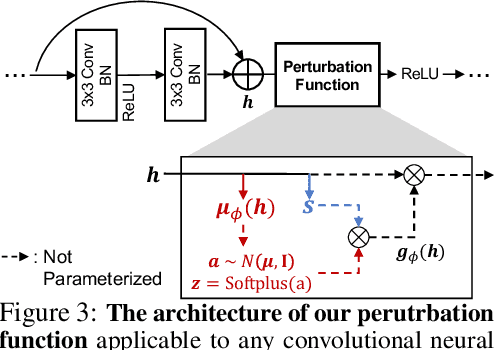
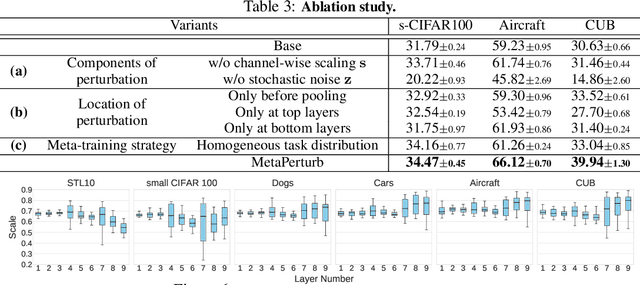
Regularization and transfer learning are two popular techniques to enhance generalization on unseen data, which is a fundamental problem of machine learning. Regularization techniques are versatile, as they are task- and architecture-agnostic, but they do not exploit a large amount of data available. Transfer learning methods learn to transfer knowledge from one domain to another, but may not generalize across tasks and architectures, and may introduce new training cost for adapting to the target task. To bridge the gap between the two, we propose a transferable perturbation, MetaPerturb, which is meta-learned to improve generalization performance on unseen data. MetaPerturb is implemented as a set-based lightweight network that is agnostic to the size and the order of the input, which is shared across the layers. Then, we propose a meta-learning framework, to jointly train the perturbation function over heterogeneous tasks in parallel. As MetaPerturb is a set-function trained over diverse distributions across layers and tasks, it can generalize to heterogeneous tasks and architectures. We validate the efficacy and generality of MetaPerturb trained on a specific source domain and architecture, by applying it to the training of diverse neural architectures on heterogeneous target datasets against various regularizers and fine-tuning. The results show that the networks trained with MetaPerturb significantly outperform the baselines on most of the tasks and architectures, with a negligible increase in the parameter size and no hyperparameters to tune.