A third-order finite difference weighted essentially non-oscillatory scheme with shallow neural network

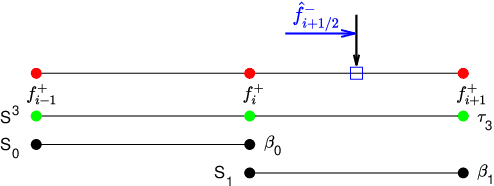
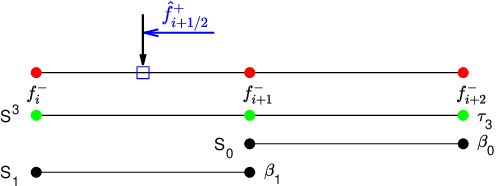
In this paper, we introduce the finite difference weighted essentially non-oscillatory (WENO) scheme based on the neural network for hyperbolic conservation laws. We employ the supervised learning and design two loss functions, one with the mean squared error and the other with the mean squared logarithmic error, where the WENO3-JS weights are computed as the labels. Each loss function consists of two components where the first component compares the difference between the weights from the neural network and WENO3-JS weights, while the second component matches the output weights of the neural network and the linear weights. The former of the loss function enforces the neural network to follow the WENO properties, implying that there is no need for the post-processing layer. Additionally the latter leads to better performance around discontinuities. As a neural network structure, we choose the shallow neural network (SNN) for computational efficiency with the Delta layer consisting of the normalized undivided differences. These constructed WENO3-SNN schemes show the outperformed results in one-dimensional examples and improved behavior in two-dimensional examples, compared with the simulations from WENO3-JS and WENO3-Z.

Filtration learning in exact multi-parameter persistent homology and classification of time-series data

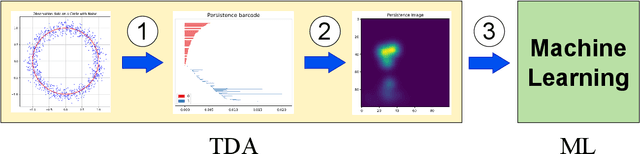
To analyze the topological properties of the given discrete data, one needs to consider a continuous transform called filtration. Persistent homology serves as a tool to track changes of homology in the filtration. The outcome of the topological analysis of data varies depending on the choice of filtration, making the selection of filtration crucial. Filtration learning is an attempt to find an optimal filtration that minimizes the loss function. Exact Multi-parameter Persistent Homology (EMPH) has been recently proposed, particularly for topological time-series analysis, that utilizes the exact formula of rank invariant instead of calculating it. In this paper, we propose a framework for filtration learning of EMPH. We formulate an optimization problem and propose an algorithm for solving the problem. We then apply the proposed algorithm to several classification problems. Particularly, we derive the exact formula of the gradient of the loss function with respect to the filtration parameter, which makes it possible to directly update the filtration without using automatic differentiation, significantly enhancing the learning process.

PHLP: Sole Persistent Homology for Link Prediction -- Interpretable Feature Extraction

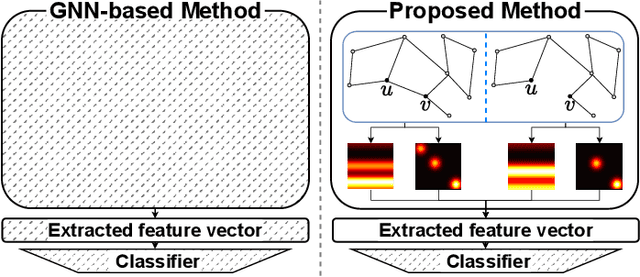
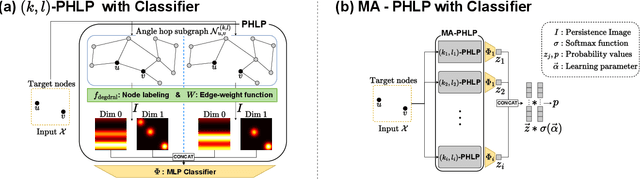
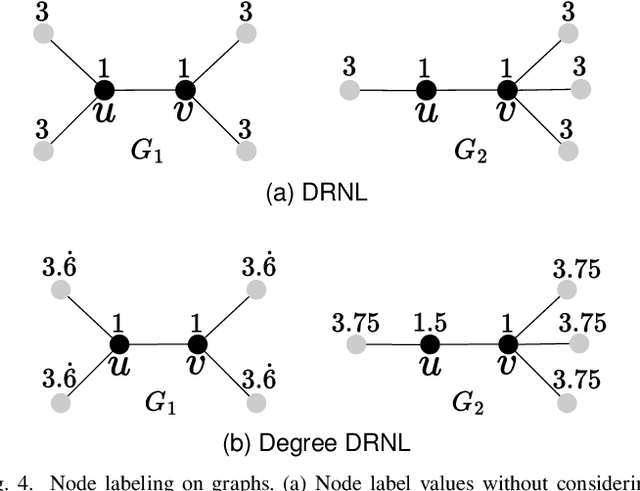
Link prediction (LP), inferring the connectivity between nodes, is a significant research area in graph data, where a link represents essential information on relationships between nodes. Although graph neural network (GNN)-based models have achieved high performance in LP, understanding why they perform well is challenging because most comprise complex neural networks. We employ persistent homology (PH), a topological data analysis method that helps analyze the topological information of graphs, to explain the reasons for the high performance. We propose a novel method that employs PH for LP (PHLP) focusing on how the presence or absence of target links influences the overall topology. The PHLP utilizes the angle hop subgraph and new node labeling called degree double radius node labeling (Degree DRNL), distinguishing the information of graphs better than DRNL. Using only a classifier, PHLP performs similarly to state-of-the-art (SOTA) models on most benchmark datasets. Incorporating the outputs calculated using PHLP into the existing GNN-based SOTA models improves performance across all benchmark datasets. To the best of our knowledge, PHLP is the first method of applying PH to LP without GNNs. The proposed approach, employing PH while not relying on neural networks, enables the identification of crucial factors for improving performance.

Supervised low-rank semi-nonnegative matrix factorization with frequency regularization for forecasting spatio-temporal data

We propose a novel methodology for forecasting spatio-temporal data using supervised semi-nonnegative matrix factorization (SSNMF) with frequency regularization. Matrix factorization is employed to decompose spatio-temporal data into spatial and temporal components. To improve clarity in the temporal patterns, we introduce a nonnegativity constraint on the time domain along with regularization in the frequency domain. Specifically, regularization in the frequency domain involves selecting features in the frequency space, making an interpretation in the frequency domain more convenient. We propose two methods in the frequency domain: soft and hard regularizations, and provide convergence guarantees to first-order stationary points of the corresponding constrained optimization problem. While our primary motivation stems from geophysical data analysis based on GRACE (Gravity Recovery and Climate Experiment) data, our methodology has the potential for wider application. Consequently, when applying our methodology to GRACE data, we find that the results with the proposed methodology are comparable to previous research in the field of geophysical sciences but offer clearer interpretability.

Machine Composition of Korean Music via Topological Data Analysis and Artificial Neural Network

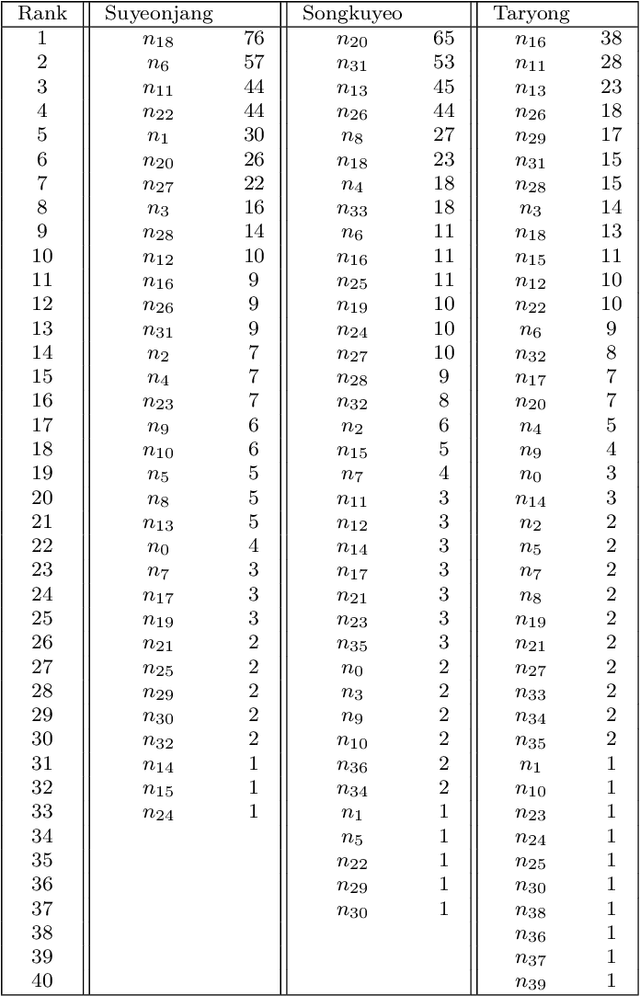
Common AI music composition algorithms based on artificial neural networks are to train a machine by feeding a large number of music pieces and create artificial neural networks that can produce music similar to the input music data. This approach is a blackbox optimization, that is, the underlying composition algorithm is, in general, not known to users. In this paper, we present a way of machine composition that trains a machine the composition principle embedded in the given music data instead of directly feeding music pieces. We propose this approach by using the concept of {\color{black}{Overlap}} matrix proposed in \cite{TPJ}. In \cite{TPJ}, a type of Korean music, so-called the {\it Dodeuri} music such as Suyeonjangjigok has been analyzed using topological data analysis (TDA), particularly using persistent homology. As the raw music data is not suitable for TDA analysis, the music data is first reconstructed as a graph. The node of the graph is defined as a two-dimensional vector composed of the pitch and duration of each music note. The edge between two nodes is created when those nodes appear consecutively in the music flow. Distance is defined based on the frequency of such appearances. Through TDA on the constructed graph, a unique set of cycles is found for the given music. In \cite{TPJ}, the new concept of the {\it {\color{black}{Overlap}} matrix} has been proposed, which visualizes how those cycles are interconnected over the music flow, in a matrix form. In this paper, we explain how we use the {\color{black}{Overlap}} matrix for machine composition. The {\color{black}{Overlap}} matrix makes it possible to compose a new music piece algorithmically and also provide a seed music towards the desired artificial neural network. In this paper, we use the {\it Dodeuri} music and explain detailed steps.

Weighted Random Cut Forest Algorithm for Anomaly Detections

Random cut forest (RCF) algorithms have been developed for anomaly detection, particularly for the anomaly detection in time-series data. The RCF algorithm is the improved version of the isolation forest algorithm. Unlike the isolation forest algorithm, the RCF algorithm has the power of determining whether the real-time input has anomaly by inserting the input in the constructed tree network. There have been developed various RCF algorithms including Robust RCF (RRCF) with which the cutting procedure is adaptively chosen probabilistically. RRCF shows better performance compared to the isolation forest as the cutting dimension is decided based on the geometric range of the data. The overall data structure is, however, not considered in the adaptive cutting algorithm with the RRCF. In this paper, we propose a new RCF, so-called the weighted RCF (WRCF). In order to introduce the WRCF, we first introduce a new geometric measure, i.e., a \textit{density measure} which is crucial for the construction of the WRCF. We provide various mathematical properties of the density measure. The proposed WRCF also cuts the tree network adaptively, but with consideration of the denseness of the data. The proposed method is more efficient when the data is structured and achieves the desired anomaly score more rapidly than the RRCF. We provide theorems that prove our claims with numerical examples.

Topological Data Analysis of Korean Music in Jeongganbo: A Cycle Structure

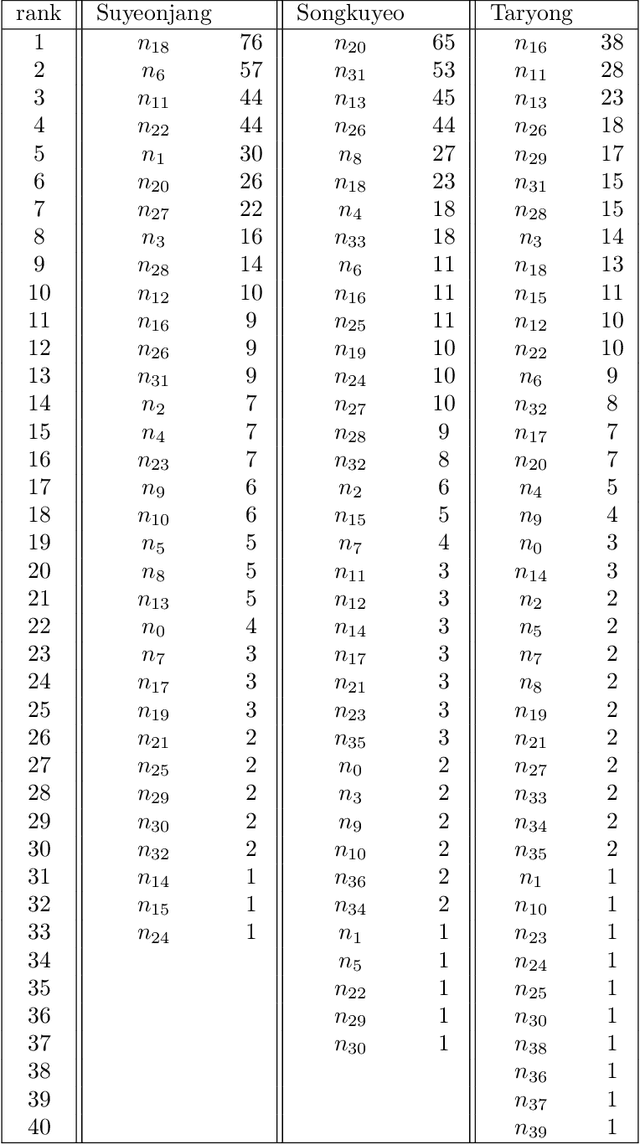
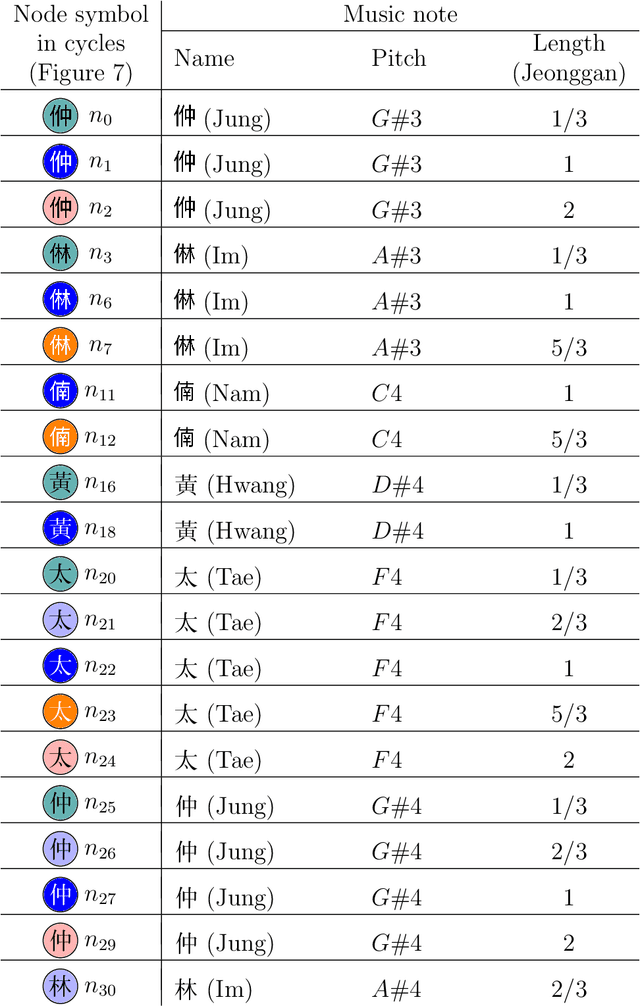
Jeongganbo is a unique music representation invented by Sejong the Great. Contrary to the western music notation, the pitch of each note is encrypted and the length is visualized directly in a matrix form in Jeongganbo. We use topological data analysis (TDA) to analyze the Korean music written in Jeongganbo for Suyeonjang, Songuyeo, and Taryong, those well-known pieces played at the palace and among noble community. We are particularly interested in the cycle structure. We first define and determine the node elements of each music, characterized uniquely with its pitch and length. Then we transform the music into a graph and define the distance between the nodes as their adjacent occurrence rate. The graph is used as a point cloud whose homological structure is investigated by measuring the hole structure in each dimension. We identify cycles of each music, match those in Jeongganbo, and show how those cycles are interconnected. The main discovery of this work is that the cycles of Suyeonjang and Songuyeo, categorized as a special type of cyclic music known as Dodeuri, frequently overlap each other when appearing in the music while the cycles found in Taryong, which does not belong to Dodeuri class, appear individually.

The Interconnectivity Vector: A Finite-Dimensional Vector Representation of Persistent Homology

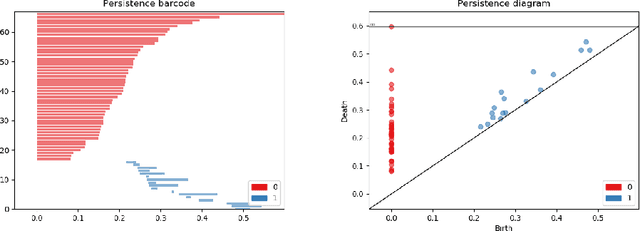
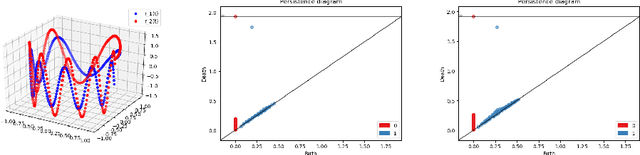
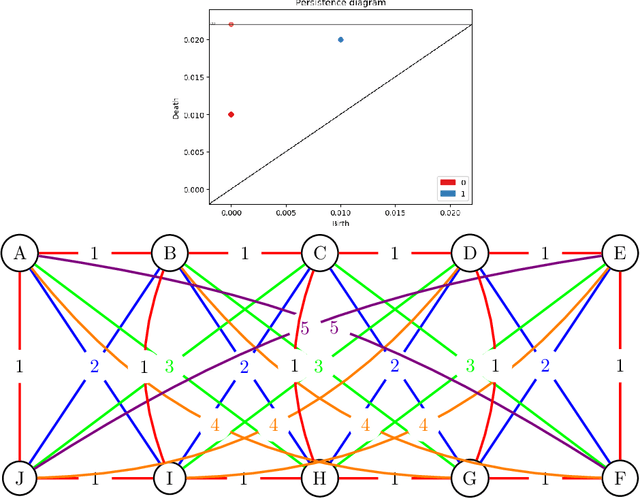
Persistent Homology (PH) is a useful tool to study the underlying structure of a data set. Persistence Diagrams (PDs), which are 2D multisets of points, are a concise summary of the information found by studying the PH of a data set. However, PDs are difficult to incorporate into a typical machine learning workflow. To that end, two main methods for representing PDs have been developed: kernel methods and vectorization methods. In this paper we propose a new finite-dimensional vector, called the interconnectivity vector, representation of a PD adapted from Bag-of-Words (BoW). This new representation is constructed to demonstrate the connections between the homological features of a data set. This initial definition of the interconnectivity vector proves to be unstable, but we introduce a stabilized version of the vector and prove its stability with respect to small perturbations in the inputs. We evaluate both versions of the presented vectorization on several data sets and show their high discriminative power.

Detection of gravitational waves using topological data analysis and convolutional neural network: An improved approach

The gravitational wave detection problem is challenging because the noise is typically overwhelming. Convolutional neural networks (CNNs) have been successfully applied, but require a large training set and the accuracy suffers significantly in the case of low SNR. We propose an improved method that employs a feature extraction step using persistent homology. The resulting method is more resilient to noise, more capable of detecting signals with varied signatures and requires less training. This is a powerful improvement as the detection problem can be computationally intense and is concerned with a relatively large class of wave signatures.