Filtration learning in exact multi-parameter persistent homology and classification of time-series data

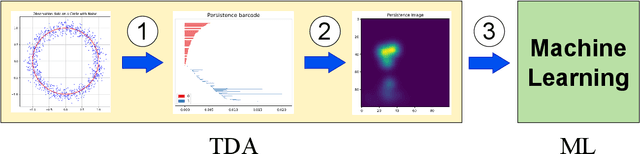
To analyze the topological properties of the given discrete data, one needs to consider a continuous transform called filtration. Persistent homology serves as a tool to track changes of homology in the filtration. The outcome of the topological analysis of data varies depending on the choice of filtration, making the selection of filtration crucial. Filtration learning is an attempt to find an optimal filtration that minimizes the loss function. Exact Multi-parameter Persistent Homology (EMPH) has been recently proposed, particularly for topological time-series analysis, that utilizes the exact formula of rank invariant instead of calculating it. In this paper, we propose a framework for filtration learning of EMPH. We formulate an optimization problem and propose an algorithm for solving the problem. We then apply the proposed algorithm to several classification problems. Particularly, we derive the exact formula of the gradient of the loss function with respect to the filtration parameter, which makes it possible to directly update the filtration without using automatic differentiation, significantly enhancing the learning process.

Supervised low-rank semi-nonnegative matrix factorization with frequency regularization for forecasting spatio-temporal data

We propose a novel methodology for forecasting spatio-temporal data using supervised semi-nonnegative matrix factorization (SSNMF) with frequency regularization. Matrix factorization is employed to decompose spatio-temporal data into spatial and temporal components. To improve clarity in the temporal patterns, we introduce a nonnegativity constraint on the time domain along with regularization in the frequency domain. Specifically, regularization in the frequency domain involves selecting features in the frequency space, making an interpretation in the frequency domain more convenient. We propose two methods in the frequency domain: soft and hard regularizations, and provide convergence guarantees to first-order stationary points of the corresponding constrained optimization problem. While our primary motivation stems from geophysical data analysis based on GRACE (Gravity Recovery and Climate Experiment) data, our methodology has the potential for wider application. Consequently, when applying our methodology to GRACE data, we find that the results with the proposed methodology are comparable to previous research in the field of geophysical sciences but offer clearer interpretability.

Highly-scalable stochastic neuron based on Ovonic Threshold Switch (OTS) and its applications in Restricted Boltzmann Machine (RBM)

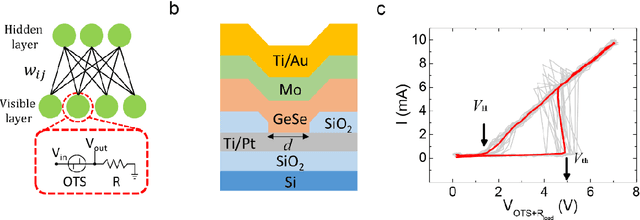
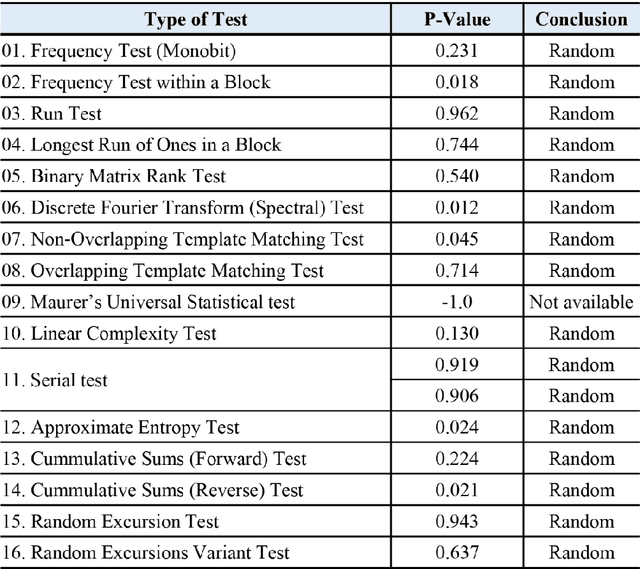
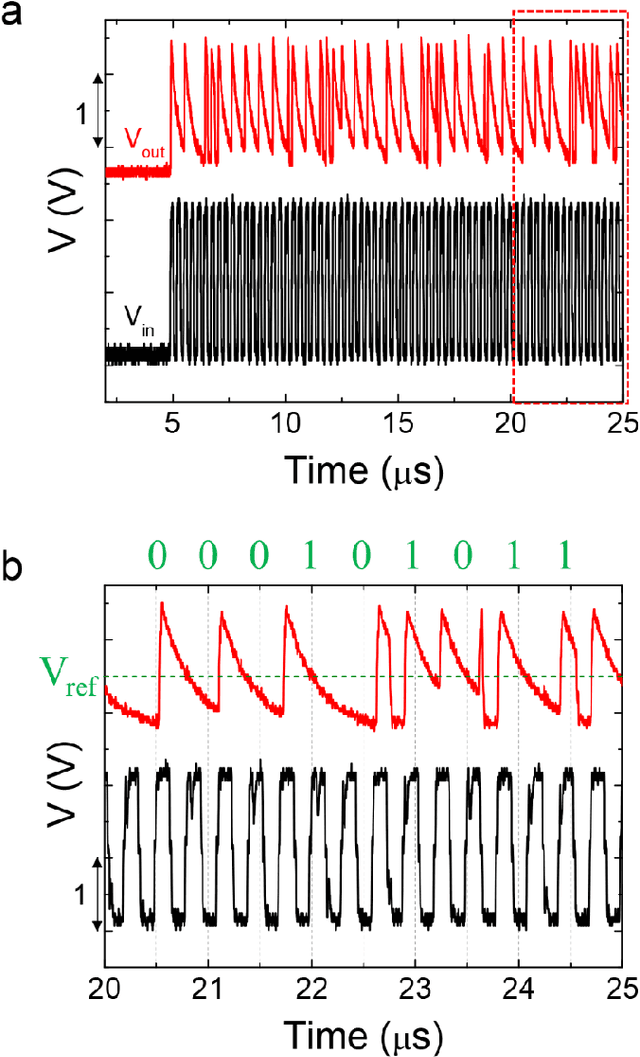
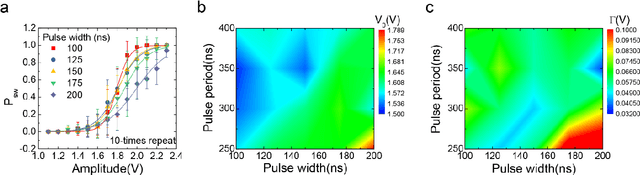
Interest in Restricted Boltzmann Machine (RBM) is growing as a generative stochastic artificial neural network to implement a novel energy-efficient machine-learning (ML) technique. For a hardware implementation of the RBM, an essential building block is a reliable stochastic binary neuron device that generates random spikes following the Boltzmann distribution. Here, we propose a highly-scalable stochastic neuron device based on Ovonic Threshold Switch (OTS) which utilizes the random emission and capture process of traps as the source of stochasticity. The switching probability is well described by the Boltzmann distribution, which can be controlled by operating parameters. As a candidate for a true random number generator (TRNG), it passes 15 among the 16 tests of the National Institute of Standards and Technology (NIST) Statistical Test Suite (Special Publication 800-22). In addition, the recognition task of handwritten digits (MNIST) is demonstrated using a simulated RBM network consisting of the proposed device with a maximum recognition accuracy of 86.07 %. Furthermore, reconstruction of images is successfully demonstrated using images contaminated with noises, resulting in images with the noise removed. These results show the promising properties of OTS-based stochastic neuron devices for applications in RBM systems.