Sijin Yeom
Weighted Random Cut Forest Algorithm for Anomaly Detections
Feb 01, 2022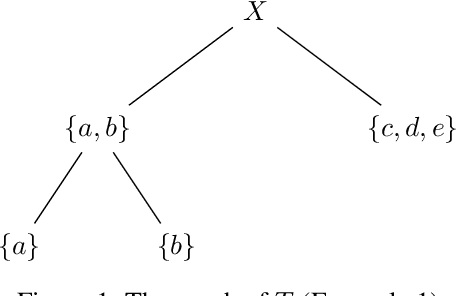

Abstract:Random cut forest (RCF) algorithms have been developed for anomaly detection, particularly for the anomaly detection in time-series data. The RCF algorithm is the improved version of the isolation forest algorithm. Unlike the isolation forest algorithm, the RCF algorithm has the power of determining whether the real-time input has anomaly by inserting the input in the constructed tree network. There have been developed various RCF algorithms including Robust RCF (RRCF) with which the cutting procedure is adaptively chosen probabilistically. RRCF shows better performance compared to the isolation forest as the cutting dimension is decided based on the geometric range of the data. The overall data structure is, however, not considered in the adaptive cutting algorithm with the RRCF. In this paper, we propose a new RCF, so-called the weighted RCF (WRCF). In order to introduce the WRCF, we first introduce a new geometric measure, i.e., a \textit{density measure} which is crucial for the construction of the WRCF. We provide various mathematical properties of the density measure. The proposed WRCF also cuts the tree network adaptively, but with consideration of the denseness of the data. The proposed method is more efficient when the data is structured and achieves the desired anomaly score more rapidly than the RRCF. We provide theorems that prove our claims with numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge