Composer 2 Technical Report

Composer 2 is a specialized model designed for agentic software engineering. The model demonstrates strong long-term planning and coding intelligence while maintaining the ability to efficiently solve problems for interactive use. The model is trained in two phases: first, continued pretraining to improve the model's knowledge and latent coding ability, followed by large-scale reinforcement learning to improve end-to-end coding performance through stronger reasoning, accurate multi-step execution, and coherence on long-horizon realistic coding problems. We develop infrastructure to support training in the same Cursor harness that is used by the deployed model, with equivalent tools and structure, and use environments that match real problems closely. To measure the ability of the model on increasingly difficult tasks, we introduce a benchmark derived from real software engineering problems in large codebases including our own. Composer 2 is a frontier-level coding model and demonstrates a process for training strong domain-specialized models. On our CursorBench evaluations the model achieves a major improvement in accuracy compared to previous Composer models (61.3). On public benchmarks the model scores 61.7 on Terminal-Bench and 73.7 on SWE-bench Multilingual in our harness, comparable to state-of-the-art systems.

An Isometric Stochastic Optimizer

The Adam optimizer is the standard choice in deep learning applications. I propose a simple explanation of Adam's success: it makes each parameter's step size independent of the norms of the other parameters. Based on this principle I derive Iso, a new optimizer which makes the norm of a parameter's update invariant to the application of any linear transformation to its inputs and outputs. I develop a variant of Iso called IsoAdam that allows optimal hyperparameters to be transferred from Adam, and demonstrate that IsoAdam obtains a speedup over Adam when training a small Transformer.

Scaling Laws for Autoregressive Generative Modeling

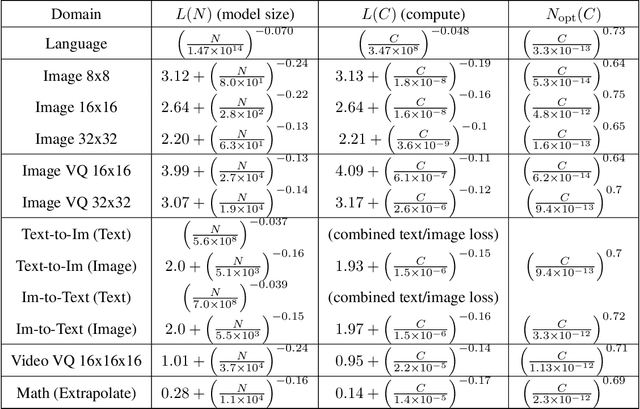
We identify empirical scaling laws for the cross-entropy loss in four domains: generative image modeling, video modeling, multimodal image$\leftrightarrow$text models, and mathematical problem solving. In all cases autoregressive Transformers smoothly improve in performance as model size and compute budgets increase, following a power-law plus constant scaling law. The optimal model size also depends on the compute budget through a power-law, with exponents that are nearly universal across all data domains. The cross-entropy loss has an information theoretic interpretation as $S($True$) + D_{\mathrm{KL}}($True$||$Model$)$, and the empirical scaling laws suggest a prediction for both the true data distribution's entropy and the KL divergence between the true and model distributions. With this interpretation, billion-parameter Transformers are nearly perfect models of the YFCC100M image distribution downsampled to an $8\times 8$ resolution, and we can forecast the model size needed to achieve any given reducible loss (ie $D_{\mathrm{KL}}$) in nats/image for other resolutions. We find a number of additional scaling laws in specific domains: (a) we identify a scaling relation for the mutual information between captions and images in multimodal models, and show how to answer the question "Is a picture worth a thousand words?"; (b) in the case of mathematical problem solving, we identify scaling laws for model performance when extrapolating beyond the training distribution; (c) we finetune generative image models for ImageNet classification and find smooth scaling of the classification loss and error rate, even as the generative loss levels off. Taken together, these results strengthen the case that scaling laws have important implications for neural network performance, including on downstream tasks.

An Empirical Study on Hyperparameters and their Interdependence for RL Generalization

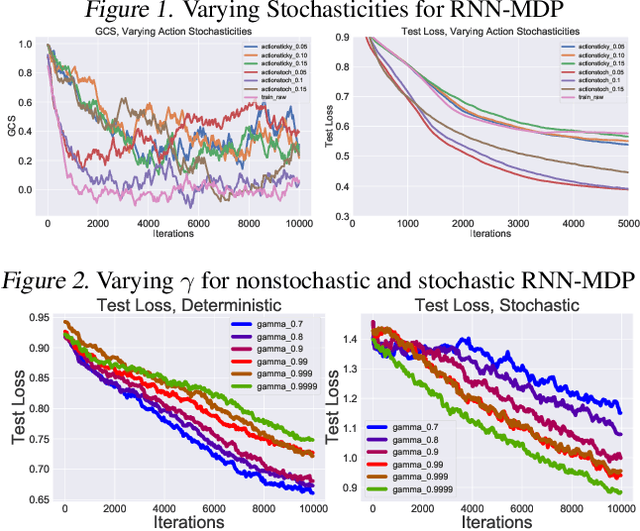
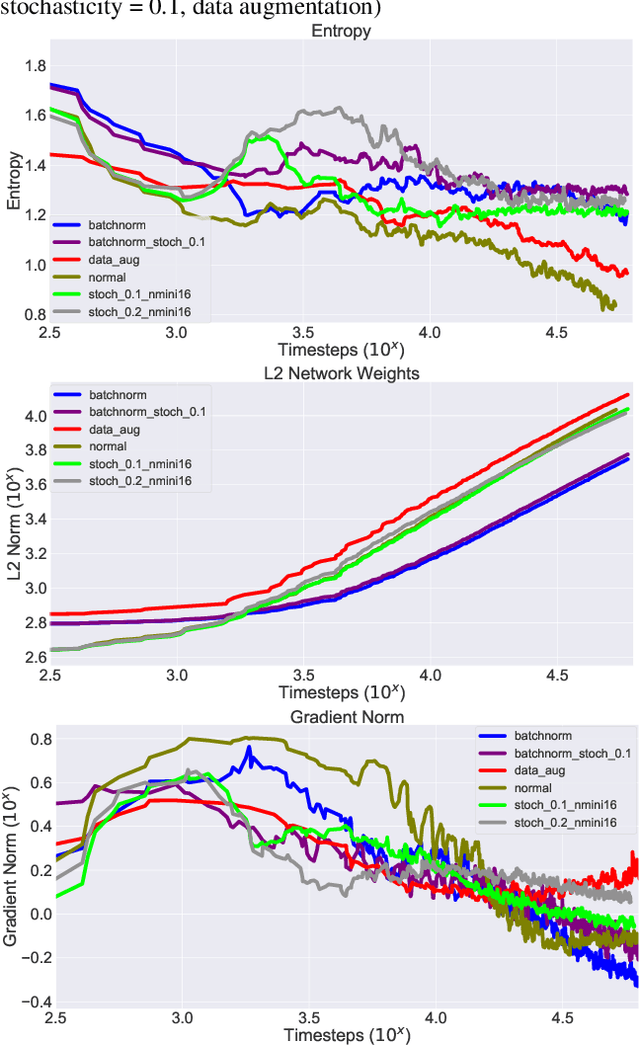
Recent results in Reinforcement Learning (RL) have shown that agents with limited training environments are susceptible to a large amount of overfitting across many domains. A key challenge for RL generalization is to quantitatively explain the effects of changing parameters on testing performance. Such parameters include architecture, regularization, and RL-dependent variables such as discount factor and action stochasticity. We provide empirical results that show complex and interdependent relationships between hyperparameters and generalization. We further show that several empirical metrics such as gradient cosine similarity and trajectory-dependent metrics serve to provide intuition towards these results.

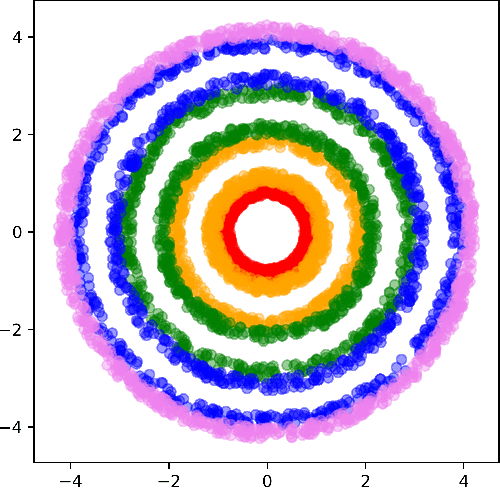
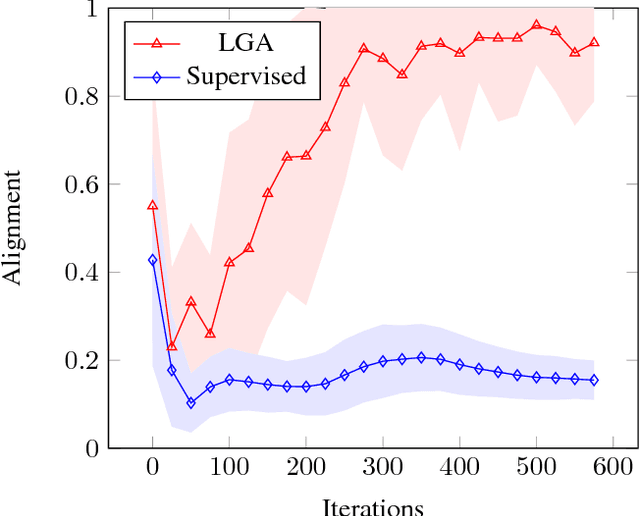
Semi-Supervised Learning by Label Gradient Alignment

We present label gradient alignment, a novel algorithm for semi-supervised learning which imputes labels for the unlabeled data and trains on the imputed labels. We define a semantically meaningful distance metric on the input space by mapping a point (x, y) to the gradient of the model at (x, y). We then formulate an optimization problem whose objective is to minimize the distance between the labeled and the unlabeled data in this space, and we solve it by gradient descent on the imputed labels. We evaluate label gradient alignment using the standardized architecture introduced by Oliver et al. (2018) and demonstrate state-of-the-art accuracy in semi-supervised CIFAR-10 classification.