Ivan Potapov
Multi-Objective Recommendation via Multivariate Policy Learning
May 03, 2024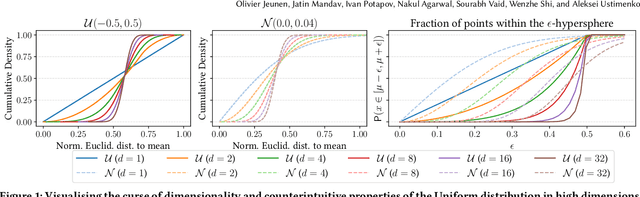

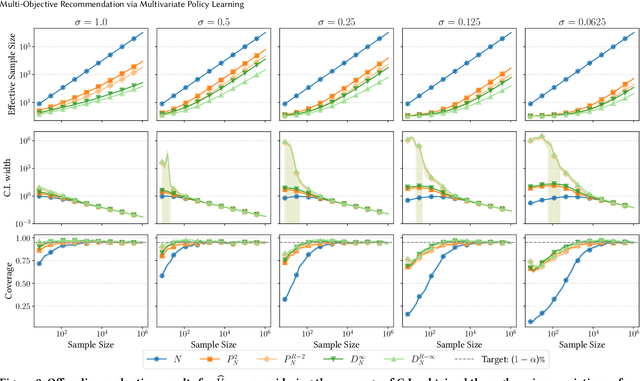
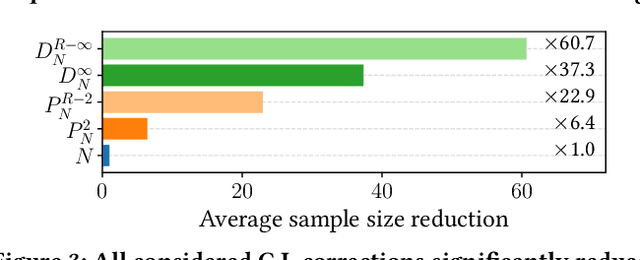
Abstract:Real-world recommender systems often need to balance multiple objectives when deciding which recommendations to present to users. These include behavioural signals (e.g. clicks, shares, dwell time), as well as broader objectives (e.g. diversity, fairness). Scalarisation methods are commonly used to handle this balancing task, where a weighted average of per-objective reward signals determines the final score used for ranking. Naturally, how these weights are computed exactly, is key to success for any online platform. We frame this as a decision-making task, where the scalarisation weights are actions taken to maximise an overall North Star reward (e.g. long-term user retention or growth). We extend existing policy learning methods to the continuous multivariate action domain, proposing to maximise a pessimistic lower bound on the North Star reward that the learnt policy will yield. Typical lower bounds based on normal approximations suffer from insufficient coverage, and we propose an efficient and effective policy-dependent correction for this. We provide guidance to design stochastic data collection policies, as well as highly sensitive reward signals. Empirical observations from simulations, offline and online experiments highlight the efficacy of our deployed approach.
On Discounted Cumulative Gain as an Offline Evaluation Metric for Top-$n$ Recommendation
Jul 27, 2023Abstract:Approaches to recommendation are typically evaluated in one of two ways: (1) via a (simulated) online experiment, often seen as the gold standard, or (2) via some offline evaluation procedure, where the goal is to approximate the outcome of an online experiment. Several offline evaluation metrics have been adopted in the literature, inspired by ranking metrics prevalent in the field of Information Retrieval. (Normalised) Discounted Cumulative Gain (nDCG) is one such metric that has seen widespread adoption in empirical studies, and higher (n)DCG values have been used to present new methods as the state-of-the-art in top-$n$ recommendation for many years. Our work takes a critical look at this approach, and investigates when we can expect such metrics to approximate the gold standard outcome of an online experiment. We formally present the assumptions that are necessary to consider DCG an unbiased estimator of online reward and provide a derivation for this metric from first principles, highlighting where we deviate from its traditional uses in IR. Importantly, we show that normalising the metric renders it inconsistent, in that even when DCG is unbiased, ranking competing methods by their normalised DCG can invert their relative order. Through a correlation analysis between off- and on-line experiments conducted on a large-scale recommendation platform, we show that our unbiased DCG estimates strongly correlate with online reward, even when some of the metric's inherent assumptions are violated. This statement no longer holds for its normalised variant, suggesting that nDCG's practical utility may be limited.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge