ISyNet: Convolutional Neural Networks design for AI accelerator

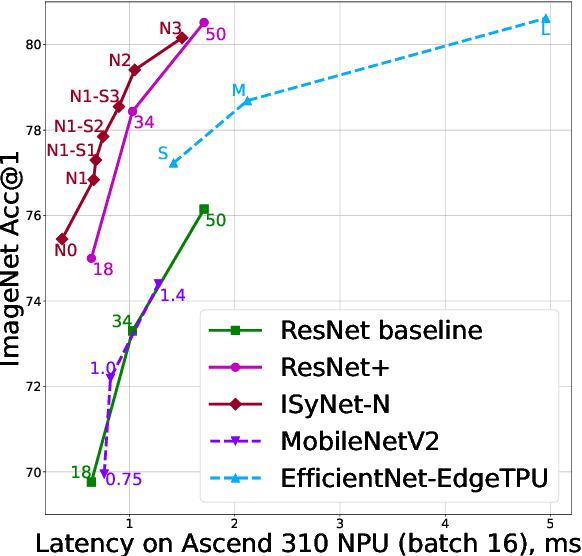
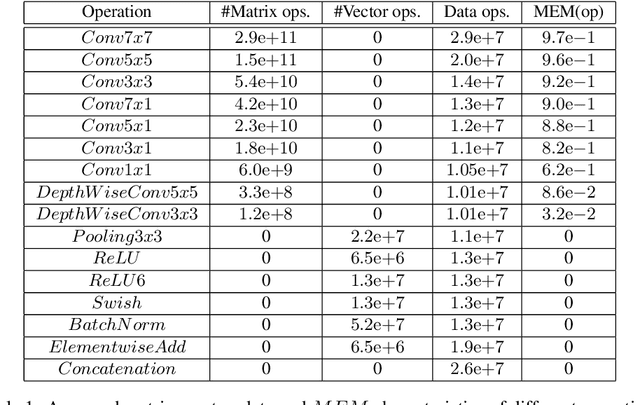
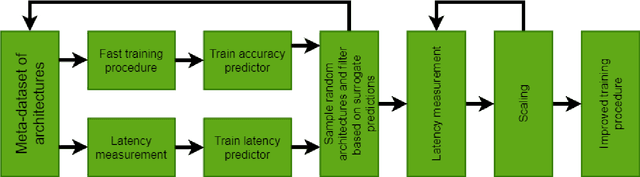
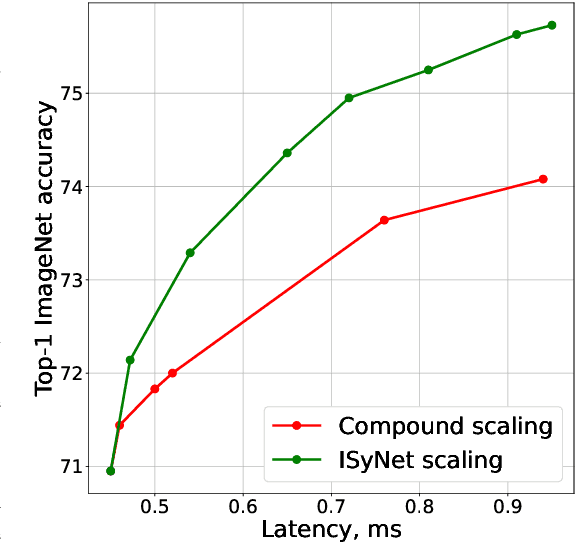
In recent years Deep Learning reached significant results in many practical problems, such as computer vision, natural language processing, speech recognition and many others. For many years the main goal of the research was to improve the quality of models, even if the complexity was impractically high. However, for the production solutions, which often require real-time work, the latency of the model plays a very important role. Current state-of-the-art architectures are found with neural architecture search (NAS) taking model complexity into account. However, designing of the search space suitable for specific hardware is still a challenging task. To address this problem we propose a measure of hardware efficiency of neural architecture search space - matrix efficiency measure (MEM); a search space comprising of hardware-efficient operations; a latency-aware scaling method; and ISyNet - a set of architectures designed to be fast on the specialized neural processing unit (NPU) hardware and accurate at the same time. We show the advantage of the designed architectures for the NPU devices on ImageNet and the generalization ability for the downstream classification and detection tasks.

Tensor Yard: One-Shot Algorithm of Hardware-Friendly Tensor-Train Decomposition for Convolutional Neural Networks

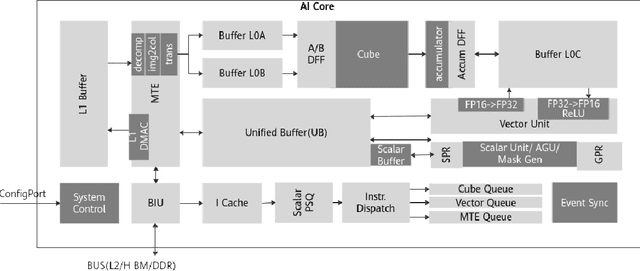
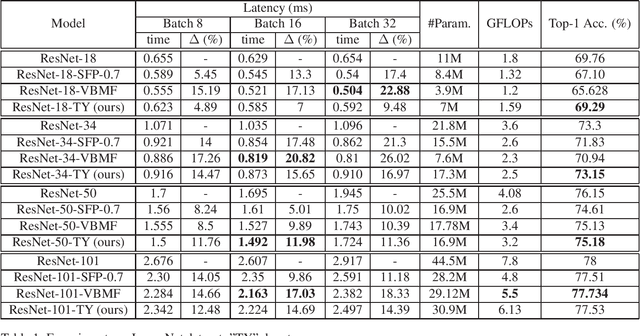
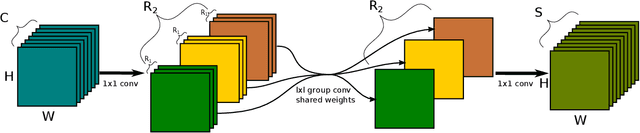
Nowadays Deep Learning became widely used in many economic, technical and scientific areas of human interest. It is clear that efficiency of solutions based on Deep Neural Networks should consider not only quality metric for the target task, but also latency and constraints of target platform design should be taken into account. In this paper we present novel hardware-friendly Tensor-Train decomposition implementation for Convolutional Neural Networks together with Tensor Yard - one-shot training algorithm which optimizes an order of decomposition of network layers. These ideas allow to accelerate ResNet models on Ascend 310 NPU devices without significant loss of accuracy. For example we accelerate ResNet-101 by 14.6% with drop by 0.5 of top-1 ImageNet accuracy.

Manifold Hypothesis in Data Analysis: Double Geometrically-Probabilistic Approach to Manifold Dimension Estimation

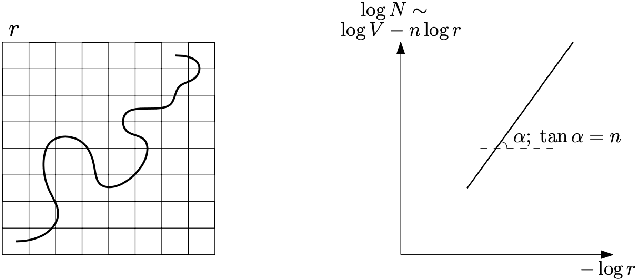
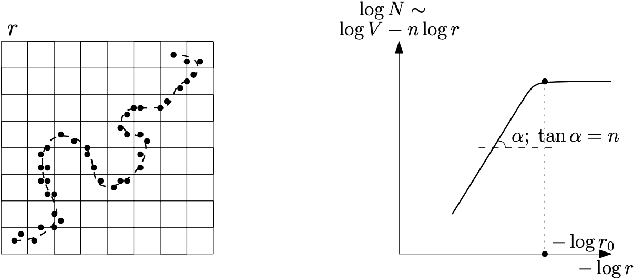
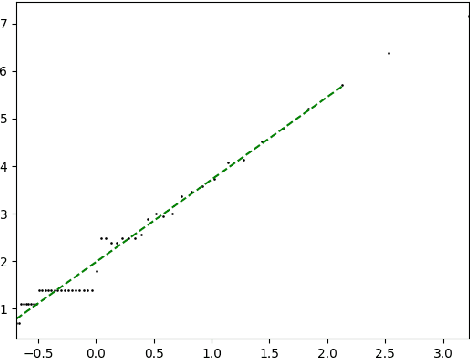
Manifold hypothesis states that data points in high-dimensional space actually lie in close vicinity of a manifold of much lower dimension. In many cases this hypothesis was empirically verified and used to enhance unsupervised and semi-supervised learning. Here we present new approach to manifold hypothesis checking and underlying manifold dimension estimation. In order to do it we use two very different methods simultaneously - one geometric, another probabilistic - and check whether they give the same result. Our geometrical method is a modification for sparse data of a well-known box-counting algorithm for Minkowski dimension calculation. The probabilistic method is new. Although it exploits standard nearest neighborhood distance, it is different from methods which were previously used in such situations. This method is robust, fast and includes special preliminary data transformation. Experiments on real datasets show that the suggested approach based on two methods combination is powerful and effective.