Issam Falih
A comparative study of emotion recognition methods using facial expressions
Dec 05, 2022
Abstract:Understanding the facial expressions of our interlocutor is important to enrich the communication and to give it a depth that goes beyond the explicitly expressed. In fact, studying one's facial expression gives insight into their hidden emotion state. However, even as humans, and despite our empathy and familiarity with the human emotional experience, we are only able to guess what the other might be feeling. In the fields of artificial intelligence and computer vision, Facial Emotion Recognition (FER) is a topic that is still in full growth mostly with the advancement of deep learning approaches and the improvement of data collection. The main purpose of this paper is to compare the performance of three state-of-the-art networks, each having their own approach to improve on FER tasks, on three FER datasets. The first and second sections respectively describe the three datasets and the three studied network architectures designed for an FER task. The experimental protocol, the results and their interpretation are outlined in the remaining sections.
Theoretical Guarantees for Domain Adaptation with Hierarchical Optimal Transport
Oct 24, 2022Abstract:Domain adaptation arises as an important problem in statistical learning theory when the data-generating processes differ between training and test samples, respectively called source and target domains. Recent theoretical advances show that the success of domain adaptation algorithms heavily relies on their ability to minimize the divergence between the probability distributions of the source and target domains. However, minimizing this divergence cannot be done independently of the minimization of other key ingredients such as the source risk or the combined error of the ideal joint hypothesis. The trade-off between these terms is often ensured by algorithmic solutions that remain implicit and not directly reflected by the theoretical guarantees. To get to the bottom of this issue, we propose in this paper a new theoretical framework for domain adaptation through hierarchical optimal transport. This framework provides more explicit generalization bounds and allows us to consider the natural hierarchical organization of samples in both domains into classes or clusters. Additionally, we provide a new divergence measure between the source and target domains called Hierarchical Wasserstein distance that indicates under mild assumptions, which structures have to be aligned to lead to a successful adaptation.
Inductive Semi-supervised Learning Through Optimal Transport
Dec 14, 2021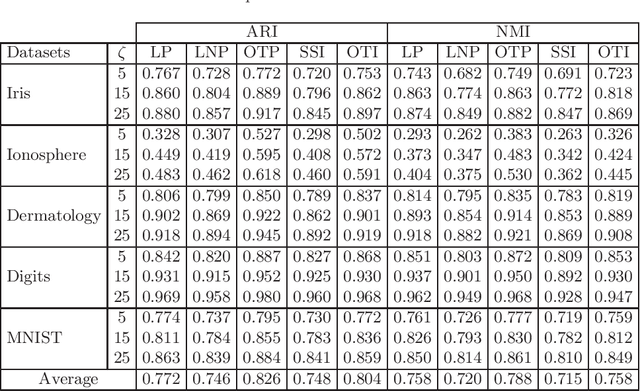
Abstract:In this paper, we tackle the inductive semi-supervised learning problem that aims to obtain label predictions for out-of-sample data. The proposed approach, called Optimal Transport Induction (OTI), extends efficiently an optimal transport based transductive algorithm (OTP) to inductive tasks for both binary and multi-class settings. A series of experiments are conducted on several datasets in order to compare the proposed approach with state-of-the-art methods. Experiments demonstrate the effectiveness of our approach. We make our code publicly available (Code is available at: https://github.com/MouradElHamri/OTI).
Hierarchical Optimal Transport for Unsupervised Domain Adaptation
Dec 03, 2021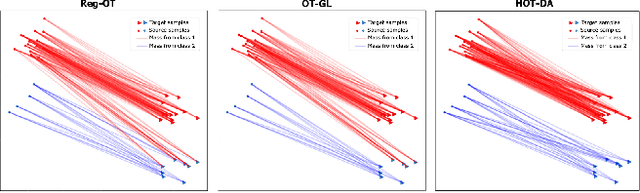
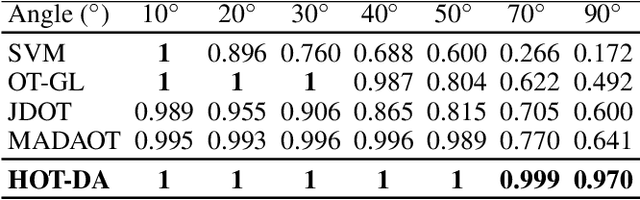
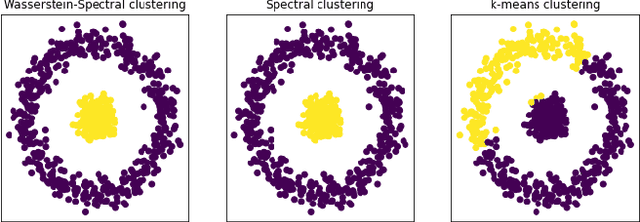
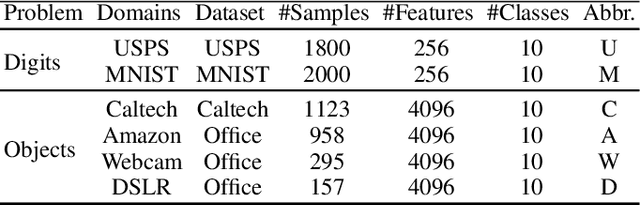
Abstract:In this paper, we propose a novel approach for unsupervised domain adaptation, that relates notions of optimal transport, learning probability measures and unsupervised learning. The proposed approach, HOT-DA, is based on a hierarchical formulation of optimal transport, that leverages beyond the geometrical information captured by the ground metric, richer structural information in the source and target domains. The additional information in the labeled source domain is formed instinctively by grouping samples into structures according to their class labels. While exploring hidden structures in the unlabeled target domain is reduced to the problem of learning probability measures through Wasserstein barycenter, which we prove to be equivalent to spectral clustering. Experiments on a toy dataset with controllable complexity and two challenging visual adaptation datasets show the superiority of the proposed approach over the state-of-the-art.
Label Propagation Through Optimal Transport
Oct 01, 2021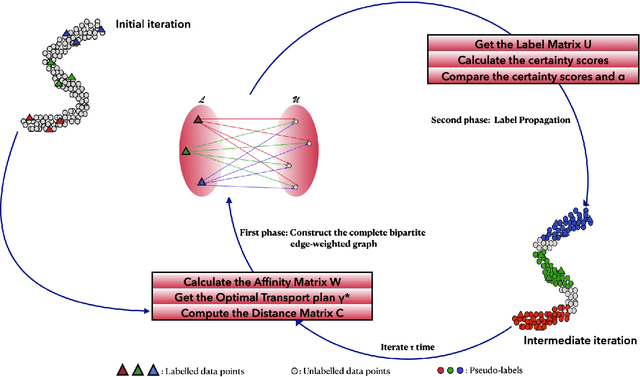


Abstract:In this paper, we tackle the transductive semi-supervised learning problem that aims to obtain label predictions for the given unlabeled data points according to Vapnik's principle. Our proposed approach is based on optimal transport, a mathematical theory that has been successfully used to address various machine learning problems, and is starting to attract renewed interest in semi-supervised learning community. The proposed approach, Optimal Transport Propagation (OTP), performs in an incremental process, label propagation through the edges of a complete bipartite edge-weighted graph, whose affinity matrix is constructed from the optimal transport plan between empirical measures defined on labeled and unlabeled data. OTP ensures a high degree of predictions certitude by controlling the propagation process using a certainty score based on Shannon's entropy. We also provide a convergence analysis of our algorithm. Experiments task show the superiority of the proposed approach over the state-of-the-art. We make our code publicly available.
* arXiv admin note: text overlap with arXiv:2103.11937
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge