Theoretical Guarantees for Domain Adaptation with Hierarchical Optimal Transport

Domain adaptation arises as an important problem in statistical learning theory when the data-generating processes differ between training and test samples, respectively called source and target domains. Recent theoretical advances show that the success of domain adaptation algorithms heavily relies on their ability to minimize the divergence between the probability distributions of the source and target domains. However, minimizing this divergence cannot be done independently of the minimization of other key ingredients such as the source risk or the combined error of the ideal joint hypothesis. The trade-off between these terms is often ensured by algorithmic solutions that remain implicit and not directly reflected by the theoretical guarantees. To get to the bottom of this issue, we propose in this paper a new theoretical framework for domain adaptation through hierarchical optimal transport. This framework provides more explicit generalization bounds and allows us to consider the natural hierarchical organization of samples in both domains into classes or clusters. Additionally, we provide a new divergence measure between the source and target domains called Hierarchical Wasserstein distance that indicates under mild assumptions, which structures have to be aligned to lead to a successful adaptation.

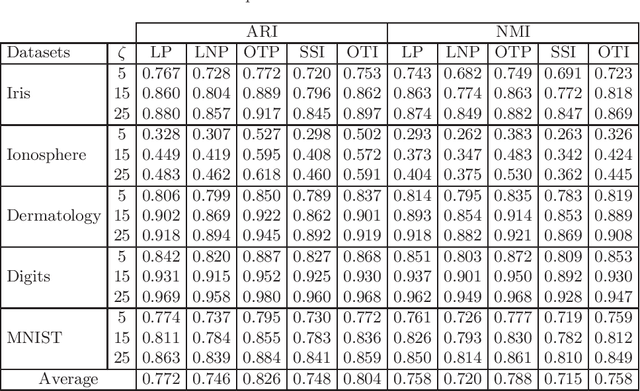
Inductive Semi-supervised Learning Through Optimal Transport

In this paper, we tackle the inductive semi-supervised learning problem that aims to obtain label predictions for out-of-sample data. The proposed approach, called Optimal Transport Induction (OTI), extends efficiently an optimal transport based transductive algorithm (OTP) to inductive tasks for both binary and multi-class settings. A series of experiments are conducted on several datasets in order to compare the proposed approach with state-of-the-art methods. Experiments demonstrate the effectiveness of our approach. We make our code publicly available (Code is available at: https://github.com/MouradElHamri/OTI).

Hierarchical Optimal Transport for Unsupervised Domain Adaptation

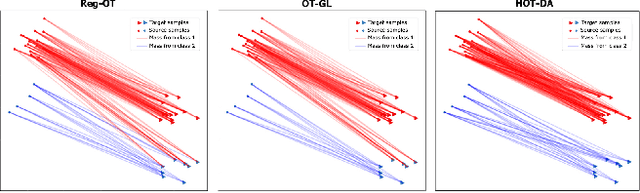
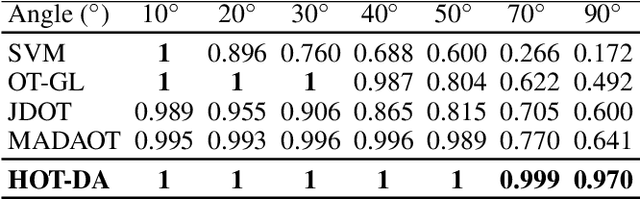
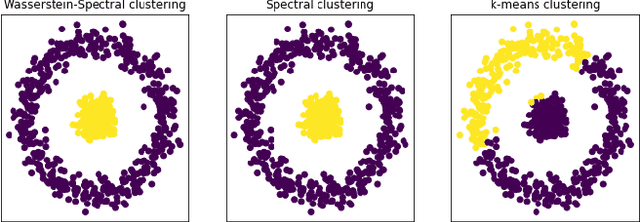
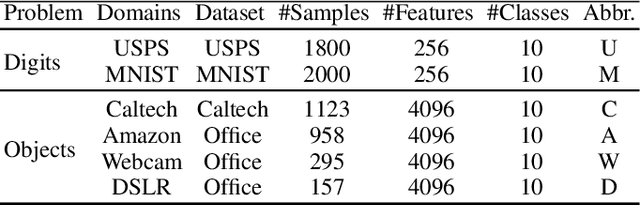
In this paper, we propose a novel approach for unsupervised domain adaptation, that relates notions of optimal transport, learning probability measures and unsupervised learning. The proposed approach, HOT-DA, is based on a hierarchical formulation of optimal transport, that leverages beyond the geometrical information captured by the ground metric, richer structural information in the source and target domains. The additional information in the labeled source domain is formed instinctively by grouping samples into structures according to their class labels. While exploring hidden structures in the unlabeled target domain is reduced to the problem of learning probability measures through Wasserstein barycenter, which we prove to be equivalent to spectral clustering. Experiments on a toy dataset with controllable complexity and two challenging visual adaptation datasets show the superiority of the proposed approach over the state-of-the-art.

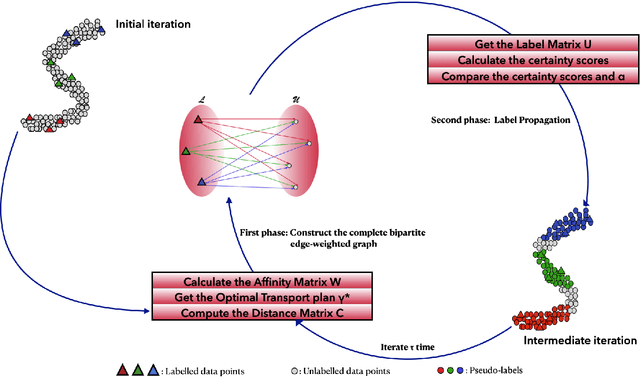
Label Propagation Through Optimal Transport

In this paper, we tackle the transductive semi-supervised learning problem that aims to obtain label predictions for the given unlabeled data points according to Vapnik's principle. Our proposed approach is based on optimal transport, a mathematical theory that has been successfully used to address various machine learning problems, and is starting to attract renewed interest in semi-supervised learning community. The proposed approach, Optimal Transport Propagation (OTP), performs in an incremental process, label propagation through the edges of a complete bipartite edge-weighted graph, whose affinity matrix is constructed from the optimal transport plan between empirical measures defined on labeled and unlabeled data. OTP ensures a high degree of predictions certitude by controlling the propagation process using a certainty score based on Shannon's entropy. We also provide a convergence analysis of our algorithm. Experiments task show the superiority of the proposed approach over the state-of-the-art. We make our code publicly available.

Regularized Optimal Transport for Dynamic Semi-supervised Learning

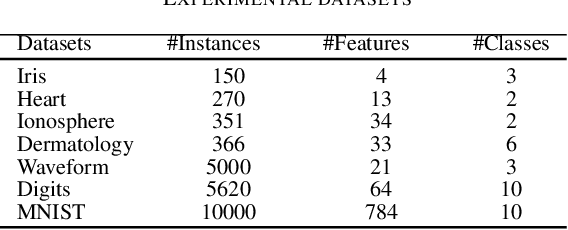
Semi-supervised learning provides an effective paradigm for leveraging unlabeled data to improve a model's performance. Among the many strategies proposed, graph-based methods have shown excellent properties, in particular since they allow to solve directly the transductive tasks according to Vapnik's principle and they can be extended efficiently for inductive tasks. In this paper, we propose a novel approach for the transductive semi-supervised learning, using a complete bipartite edge-weighted graph. The proposed approach uses the regularized optimal transport between empirical measures defined on labelled and unlabelled data points in order to obtain an affinity matrix from the optimal transport plan. This matrix is further used to propagate labels through the vertices of the graph in an incremental process ensuring the certainty of the predictions by incorporating a certainty score based on Shannon's entropy. We also analyze the convergence of our approach and we derive an efficient way to extend it for out-of-sample data. Experimental analysis was used to compare the proposed approach with other label propagation algorithms on 12 benchmark datasets, for which we surpass state-of-the-art results. We release our code.