Label Propagation Through Optimal Transport
Paper and Code
Oct 01, 2021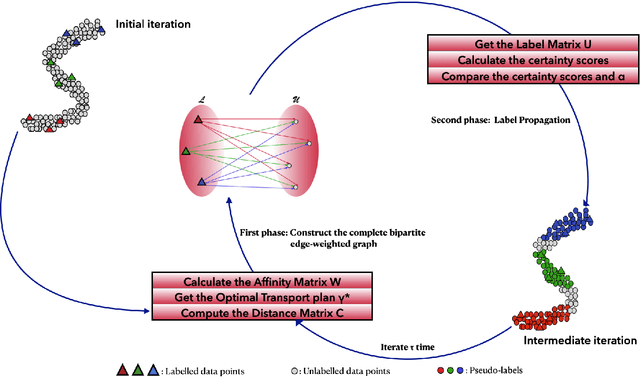


In this paper, we tackle the transductive semi-supervised learning problem that aims to obtain label predictions for the given unlabeled data points according to Vapnik's principle. Our proposed approach is based on optimal transport, a mathematical theory that has been successfully used to address various machine learning problems, and is starting to attract renewed interest in semi-supervised learning community. The proposed approach, Optimal Transport Propagation (OTP), performs in an incremental process, label propagation through the edges of a complete bipartite edge-weighted graph, whose affinity matrix is constructed from the optimal transport plan between empirical measures defined on labeled and unlabeled data. OTP ensures a high degree of predictions certitude by controlling the propagation process using a certainty score based on Shannon's entropy. We also provide a convergence analysis of our algorithm. Experiments task show the superiority of the proposed approach over the state-of-the-art. We make our code publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge