Project Auto-World: Towards Automated Benchmarking of Neural Relational Reasoners

Reasoning about relational structures remains a significant challenge for neural models, particularly when they must systematically apply learned knowledge to problem instances that are harder than those seen in training. Progress is hampered by the difficulty of evaluating such generalization, since a priori, it is rarely clear what makes an instance hard. We study how this issue can be addressed by using large language models (LLMs) to automate benchmark generation, learning to produce increasingly challenging instances in an end-to-end manner. Concretely, given a world parametrized by Datalog rules, and an Edge Transformer as the reasoning evaluator, we use LLM-driven evolutionary search (based on FunSearch) and autonomous agentic search to discover sampling functions that yield hard problem instances. We also show that the Edge Transformer can be improved using this data such that it generalizes well to further data perturbations. Finally, we show that the same machinery can be applied to novel worlds proposed by LLMs, opening the door to autonomous research on neural relational reasoning.

Benchmarking Systematic Relational Reasoning with Large Language and Reasoning Models

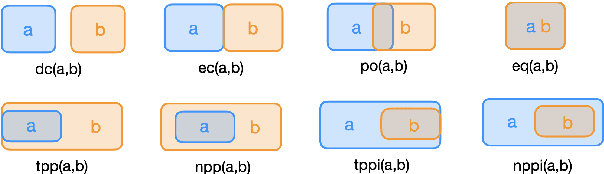
Large Language Models (LLMs) have been found to struggle with systematic reasoning. Even on tasks where they appear to perform well, their performance often depends on shortcuts, rather than on genuine reasoning abilities, leading them to collapse on out-of-distribution examples. Post-training strategies based on reinforcement learning and chain-of-thought prompting have recently been hailed as a step change. However, little is still known about the potential of the resulting ``Large Reasoning Models'' (LRMs) beyond problem solving in mathematics and programming, where finding genuine out-of-distribution problems can be difficult. In this paper, we focus on tasks that require systematic reasoning about relational compositions, especially for qualitative spatial and temporal reasoning. These tasks allow us to control the difficulty of problem instances, and measure in a precise way to what extent models can generalise. We find that that the considered LLMs and LRMs overall perform poorly overall, albeit better than random chance.

Shifting Perspectives: Steering Vector Ensembles for Robust Bias Mitigation in LLMs

We present a novel approach to bias mitigation in large language models (LLMs) by applying steering vectors to modify model activations in forward passes. We employ Bayesian optimization to systematically identify effective contrastive pair datasets across nine bias axes. When optimized on the BBQ dataset, our individually tuned steering vectors achieve average improvements of 12.2%, 4.7%, and 3.2% over the baseline for Mistral, Llama, and Qwen, respectively. Building on these promising results, we introduce Steering Vector Ensembles (SVE), a method that averages multiple individually optimized steering vectors, each targeting a specific bias axis such as age, race, or gender. By leveraging their collective strength, SVE outperforms individual steering vectors in both bias reduction and maintaining model performance. The work presents the first systematic investigation of steering vectors for bias mitigation, and we demonstrate that SVE is a powerful and computationally efficient strategy for reducing bias in LLMs, with broader implications for enhancing AI safety.

Systematic Reasoning About Relational Domains With Graph Neural Networks

Developing models that can learn to reason is a notoriously challenging problem. We focus on reasoning in relational domains, where the use of Graph Neural Networks (GNNs) seems like a natural choice. However, previous work on reasoning with GNNs has shown that such models tend to fail when presented with test examples that require longer inference chains than those seen during training. This suggests that GNNs lack the ability to generalize from training examples in a systematic way, which would fundamentally limit their reasoning abilities. A common solution is to instead rely on neuro-symbolic methods, which are capable of reasoning in a systematic way by design. Unfortunately, the scalability of such methods is often limited and they tend to rely on overly strong assumptions, e.g.\ that queries can be answered by inspecting a single relational path. In this paper, we revisit the idea of reasoning with GNNs, showing that systematic generalization is possible as long as the right inductive bias is provided. In particular, we argue that node embeddings should be treated as epistemic states and that GNN should be parameterised accordingly. We propose a simple GNN architecture which is based on this view and show that it is capable of achieving state-of-the-art results. We furthermore introduce a benchmark which requires models to aggregate evidence from multiple relational paths. We show that existing neuro-symbolic approaches fail on this benchmark, whereas our considered GNN model learns to reason accurately.

Sample-efficient Model-based Reinforcement Learning for Quantum Control

We propose a model-based reinforcement learning (RL) approach for noisy time-dependent gate optimization with improved sample complexity over model-free RL. Sample complexity is the number of controller interactions with the physical system. Leveraging an inductive bias, inspired by recent advances in neural ordinary differential equations (ODEs), we use an auto-differentiable ODE parametrised by a learnable Hamiltonian ansatz to represent the model approximating the environment whose time-dependent part, including the control, is fully known. Control alongside Hamiltonian learning of continuous time-independent parameters is addressed through interactions with the system. We demonstrate an order of magnitude advantage in the sample complexity of our method over standard model-free RL in preparing some standard unitary gates with closed and open system dynamics, in realistic numerical experiments incorporating single shot measurements, arbitrary Hilbert space truncations and uncertainty in Hamiltonian parameters. Also, the learned Hamiltonian can be leveraged by existing control methods like GRAPE for further gradient-based optimization with the controllers found by RL as initializations. Our algorithm that we apply on nitrogen vacancy (NV) centers and transmons in this paper is well suited for controlling partially characterised one and two qubit systems.