Modeling and In-flight Torso Attitude Stabilization of a Jumping Quadruped

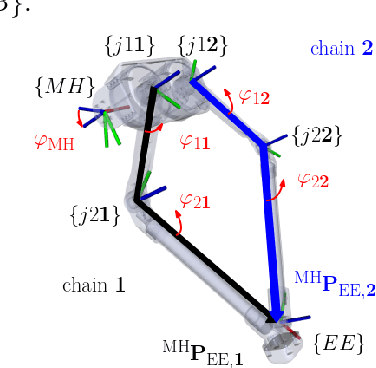
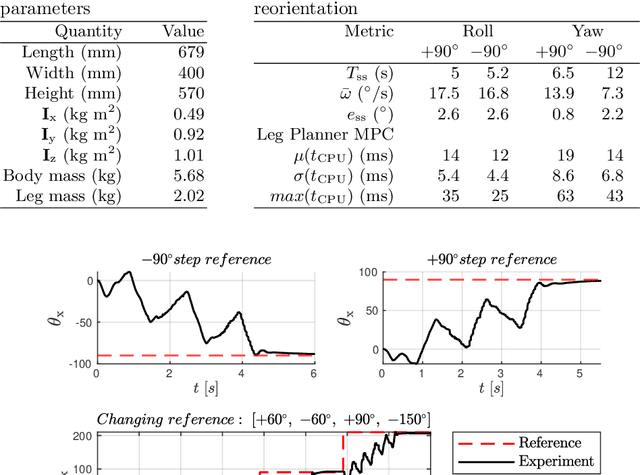
This paper addresses the modeling and attitude control of jumping quadrupeds in low-gravity environments. First, a convex decomposition procedure is presented to generate high-accuracy and low-cost collision geometries for quadrupeds performing agile maneuvers. A hierarchical control architecture is then investigated, separating torso orientation tracking from the generation of suitable, collision-free, corresponding leg motions. Nonlinear Model Predictive Controllers (NMPCs) are utilized in both layers of the controller. To compute the necessary leg motions, a torque allocation strategy is employed that leverages the symmetries of the system to avoid self-collisions and simplify the respective NMPC. To plan periodic trajectories online, a Finite State Machine (FSM)-based weight switching strategy is also used. The proposed controller is first evaluated in simulation, where 90 degree rotations in roll, pitch, and yaw are stabilized in 6.3, 2.4, and 5.5 seconds, respectively. The performance of the controller is further experimentally demonstrated by stabilizing constant and changing orientation references. Overall, this work provides a framework for the development of advanced model-based attitude controllers for jumping legged systems.

Overtaking Moving Obstacles with Digit: Path Following for Bipedal Robots via Model Predictive Contouring Control

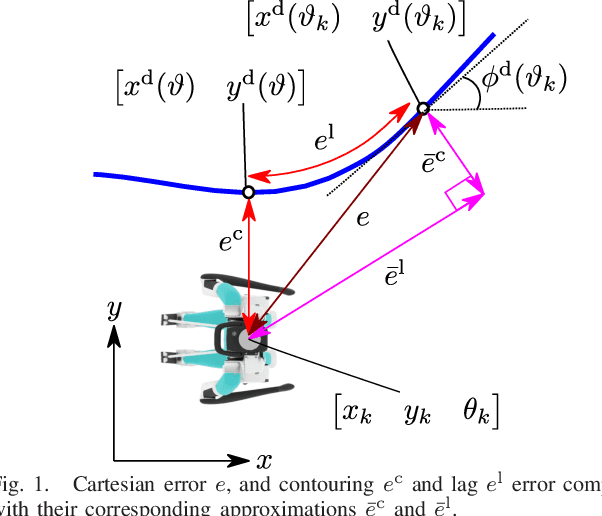
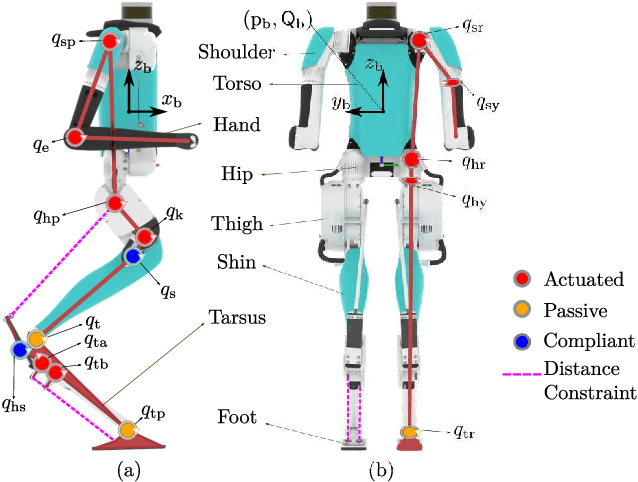
Humanoid robots are expected to navigate in changing environments and perform a variety of tasks. Frequently, these tasks require the robot to make decisions online regarding the speed and precision of following a reference path. For example, a robot may want to decide to temporarily deviate from its path to overtake a slowly moving obstacle that shares the same path and is ahead. In this case, path following performance is compromised in favor of fast path traversal. Available global trajectory tracking approaches typically assume a given -- specified in advance -- time parametrization of the path and seek to minimize the norm of the Cartesian error. As a result, when the robot should be where on the path is fixed and temporary deviations from the path are strongly discouraged. Given a global path, this paper presents a Model Predictive Contouring Control (MPCC) approach to selecting footsteps that maximize path traversal while simultaneously allowing the robot to decide between faithful versus fast path following. The method is evaluated in high-fidelity simulations of the bipedal robot Digit in terms of tracking performance of curved paths under disturbances and is also applied to the case where Digit overtakes a moving obstacle.

Reactive Gait Composition with Stability: Dynamic Walking amidst Static and Moving Obstacles

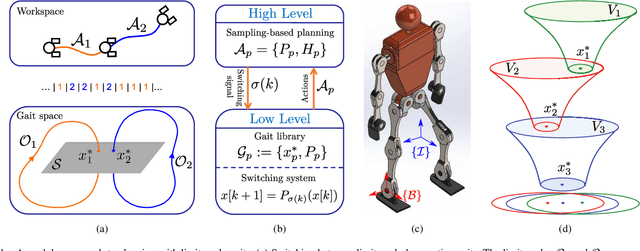
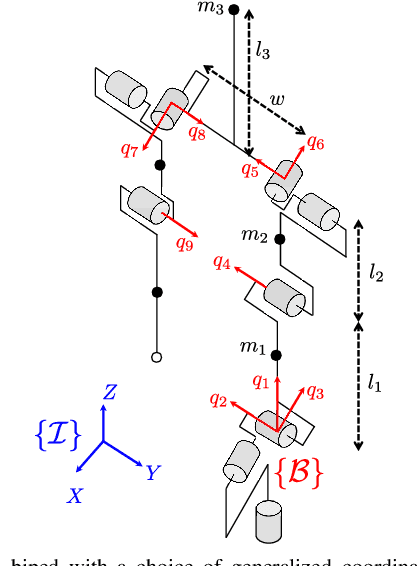
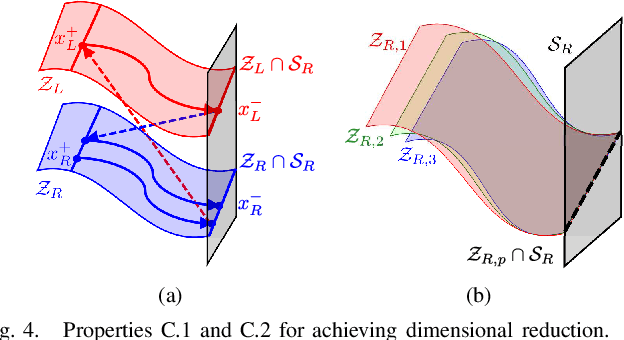
This paper presents a modular approach to motion planning with provable stability guarantees for robots that move through changing environments via periodic locomotion behaviors. We focus on dynamic walkers as a paradigm for such systems, although the tools developed in this paper can be used to support general compositional approaches to robot motion planning with Dynamic Movement Primitives (DMPs). Our approach ensures a priori that the suggested plan can be stably executed. This is achieved by formulating the planning process as a Switching System with Multiple Equilibria (SSME) and proving that the system's evolution remains within explicitly characterized trapping regions in the state space under suitable constraints on the frequency of switching among the DMPs. These conditions effectively encapsulate the low-level stability limitations in a form that can be easily communicated to the planner to guarantee that the suggested plan is compatible with the robot's dynamics. Furthermore, we show how the available primitives can be safely composed online in a receding horizon manner to enable the robot to react to moving obstacles. The proposed framework is applied on 3D bipedal walking models under common modeling assumptions, and offers a modular approach towards stably integrating readily available low-level locomotion control and high-level planning methods.

A Sequential MPC Approach to Reactive Planning for Bipedal Robots

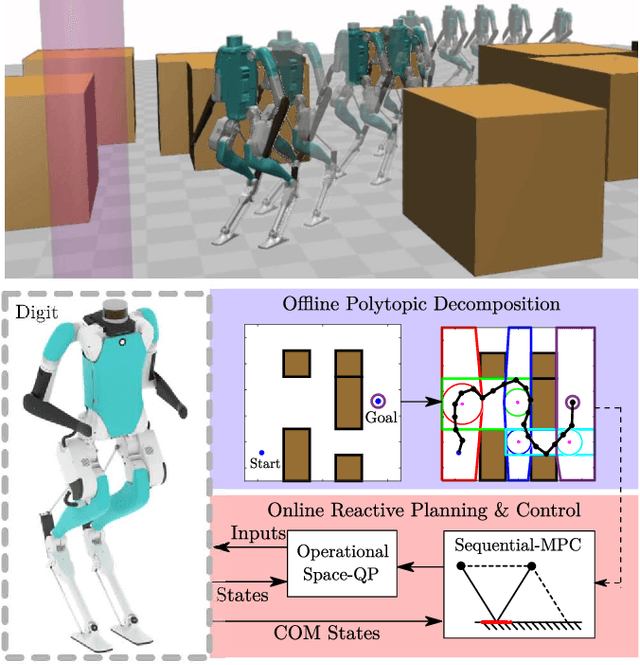
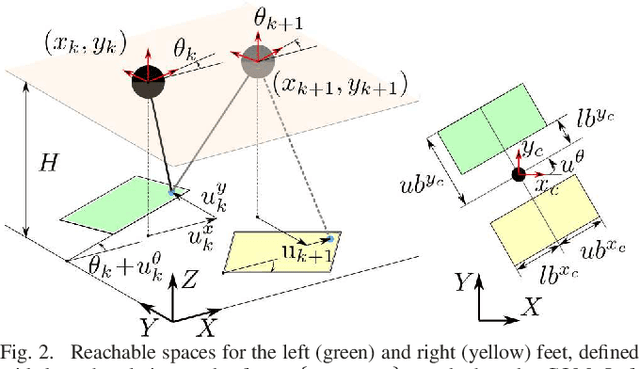
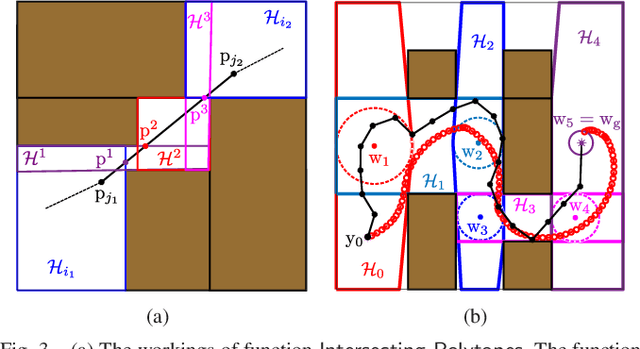
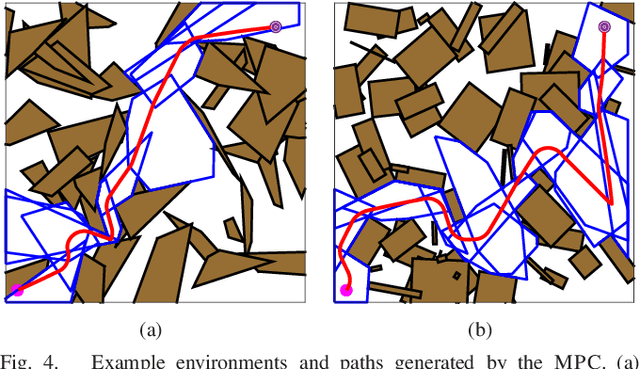
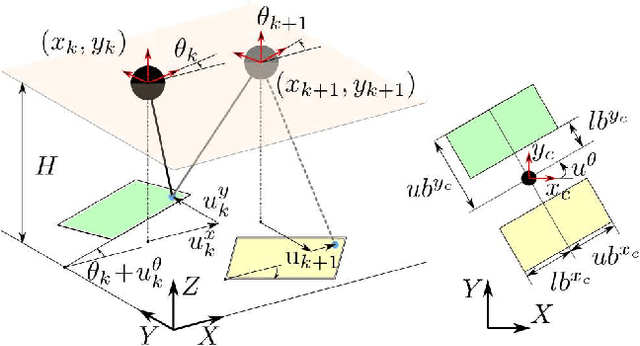
This paper presents a sequential Model Predictive Control (MPC) approach to reactive motion planning for bipedal robots in dynamic environments. The approach relies on a sequential polytopic decomposition of the free space, which provides an ordered collection of mutually intersecting obstacle free polytopes and waypoints. These are subsequently used to define a corresponding sequence of MPC programs that drive the system to a goal location avoiding static and moving obstacles. This way, the planner focuses on the free space in the vicinity of the robot, thus alleviating the need to consider all the obstacles simultaneously and reducing computational time. We verify the efficacy of our approach in high-fidelity simulations with the bipedal robot Digit, demonstrating robust reactive planning in the presence of static and moving obstacles.

Robust Dynamic Walking for a 3D Dual-SLIP Model under One-Step Unilateral Stiffness Perturbations: Towards Bipedal Locomotion over Compliant Terrain

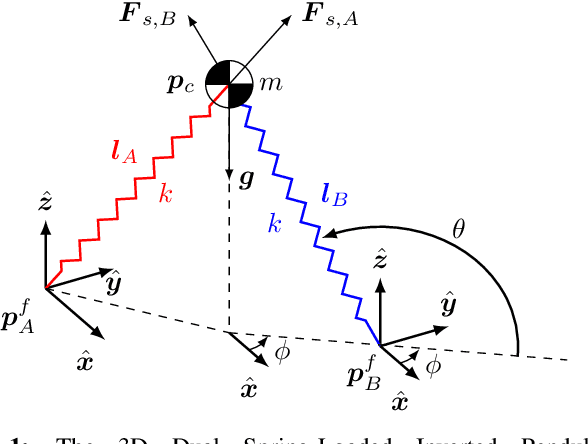
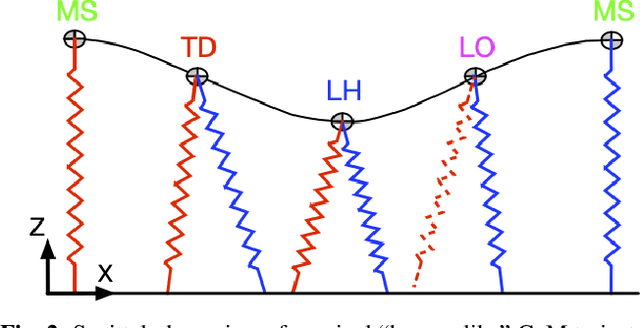
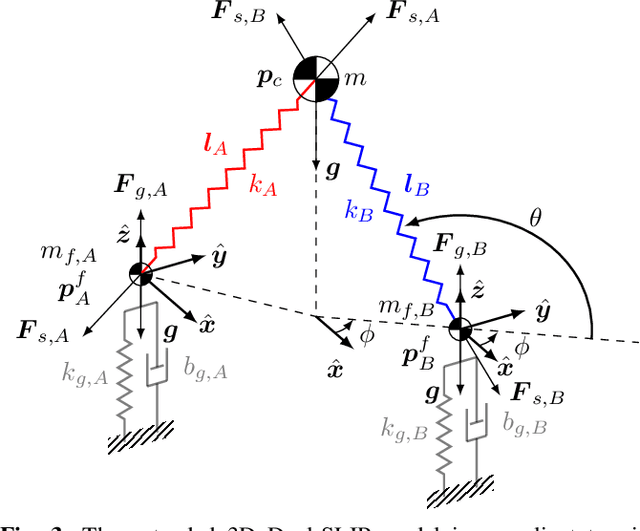
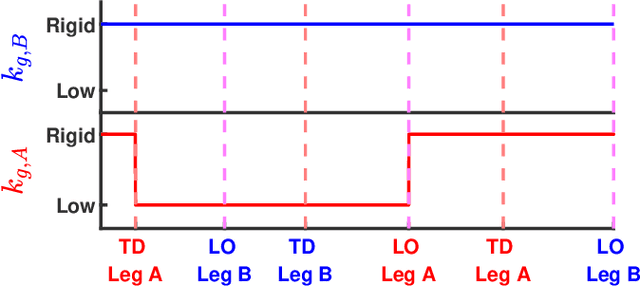
Bipedal walking is one of the most important hallmarks of human that robots have been trying to mimic for many decades. Although previous control methodologies have achieved robot walking on some terrains, there is a need for a framework allowing stable and robust locomotion over a wide range of compliant surfaces. This work proposes a novel biomechanics-inspired controller that adjusts the stiffness of the legs in support for robust and dynamic bipedal locomotion over compliant terrains. First, the 3D Dual-SLIP model is extended to support for the first time locomotion over compliant surfaces with variable stiffness and damping parameters. Then, the proposed controller is compared to a Linear-Quadratic Regulator (LQR) controller, in terms of robustness on stepping on soft terrain. The LQR controller is shown to be robust only up to a moderate ground stiffness level of 174 kN/m, while it fails in lower stiffness levels. On the contrary, the proposed controller can produce stable gait in stiffness levels as low as 30 kN/m, which results in a vertical ground penetration of the leg that is deeper than 10% of its rest length. The proposed framework could advance the field of bipedal walking, by generating stable walking trajectories for a wide range of compliant terrains useful for the control of bipeds and humanoids, as well as by improving controllers for prosthetic devices with tunable stiffness.

Interactive Dynamic Walking: Learning Gait Switching Policies with Generalization Guarantees

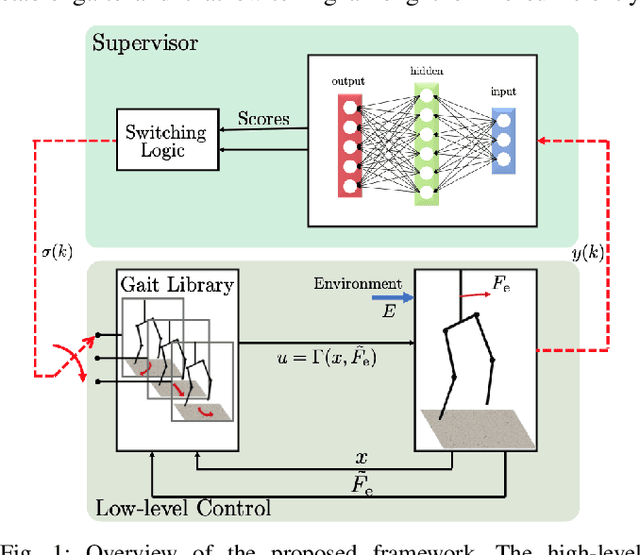
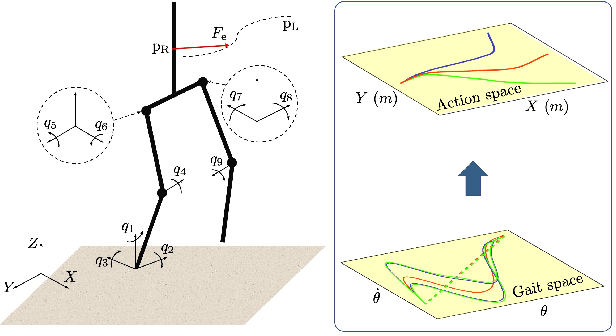
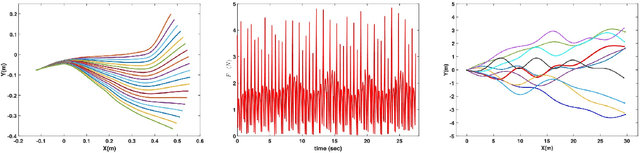
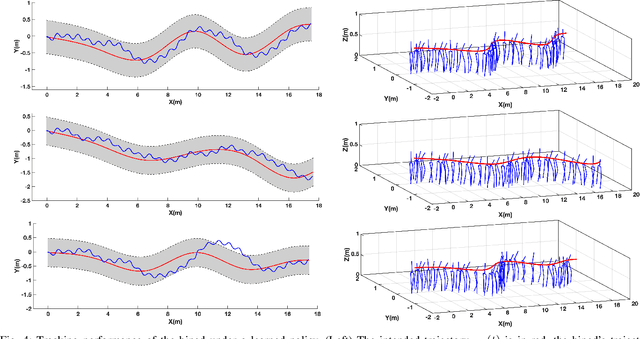
In this paper, we consider the problem of adapting a dynamically walking bipedal robot to follow a leading co-worker while engaging in tasks that require physical interaction. Our approach relies on switching among a family of Dynamic Movement Primitives (DMPs) as governed by a supervisor. We train the supervisor to orchestrate the switching among the DMPs in order to adapt to the leader's intentions, which are only implicitly available in the form of interaction forces. The primary contribution of our approach is its ability to furnish certificates of generalization to novel leader intentions for the trained supervisor. This is achieved by leveraging the Probably Approximately Correct (PAC)-Bayes bounds from generalization theory. We demonstrate the efficacy of our approach by training a neural-network supervisor to adapt the gait of a dynamically walking biped to a leading collaborator whose intended trajectory is not known explicitly.

Safe Adaptive Switching among Dynamical Movement Primitives: Application to 3D Limit-Cycle Walkers

Complex motions for robots are frequently generated by switching among a collection of individual movement primitives. We use this approach to formulate robot motion plans as sequences of primitives to be executed one after the other. When dealing with dynamical movement primitives, besides accomplishing the high-level objective, planners must also reason about the effect of the plan's execution on the safety of the platform. This task becomes more daunting in the presence of disturbances, such as external forces. To alleviate this issue, we present a framework that builds on rigorous control-theoretic tools to generate safely-executable motion plans for externally excited robotic systems. Our framework is illustrated on a 3D limit-cycle gait bipedal robot that adapts its walking pattern to persistent external forcing.

Networked Decision Making for Poisson Processes: Application to nuclear detection

This paper addresses a detection problem where several spatially distributed sensors independently observe a time-inhomogeneous stochastic process. The task is to decide between two hypotheses regarding the statistics of the observed process at the end of a fixed time interval. In the proposed method, each of the sensors transmits once to a fusion center a locally processed summary of its information in the form of a likelihood ratio. The fusion center then combines these messages to arrive at an optimal decision in the Neyman-Pearson framework. The approach is motivated by applications arising in the detection of mobile radioactive sources, and offers a pathway toward the development of novel fixed- interval detection algorithms that combine decentralized processing with optimal centralized decision making.