Reactive Gait Composition with Stability: Dynamic Walking amidst Static and Moving Obstacles
Paper and Code
Mar 28, 2023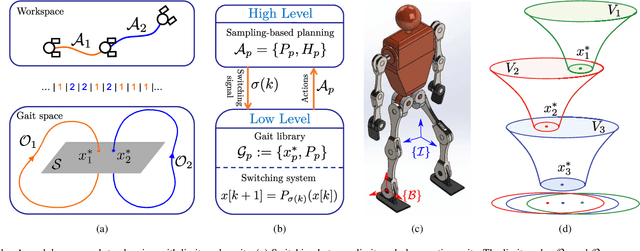

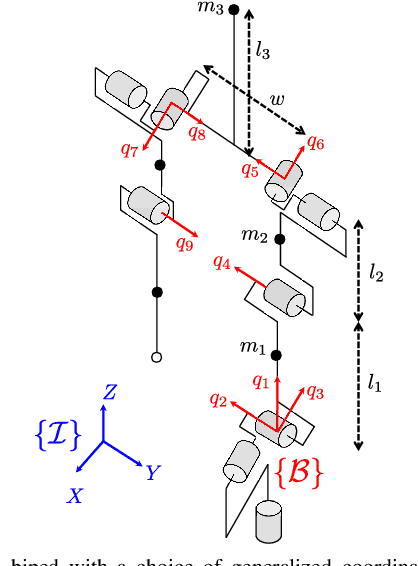
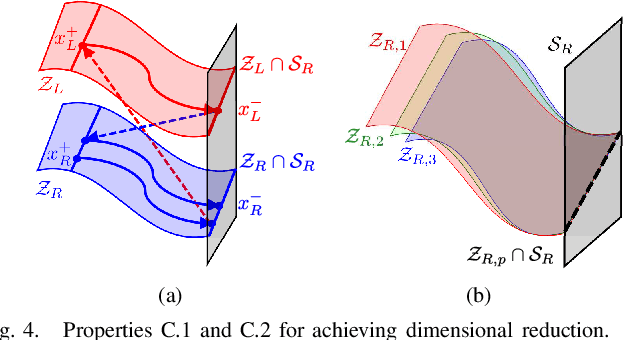
This paper presents a modular approach to motion planning with provable stability guarantees for robots that move through changing environments via periodic locomotion behaviors. We focus on dynamic walkers as a paradigm for such systems, although the tools developed in this paper can be used to support general compositional approaches to robot motion planning with Dynamic Movement Primitives (DMPs). Our approach ensures a priori that the suggested plan can be stably executed. This is achieved by formulating the planning process as a Switching System with Multiple Equilibria (SSME) and proving that the system's evolution remains within explicitly characterized trapping regions in the state space under suitable constraints on the frequency of switching among the DMPs. These conditions effectively encapsulate the low-level stability limitations in a form that can be easily communicated to the planner to guarantee that the suggested plan is compatible with the robot's dynamics. Furthermore, we show how the available primitives can be safely composed online in a receding horizon manner to enable the robot to react to moving obstacles. The proposed framework is applied on 3D bipedal walking models under common modeling assumptions, and offers a modular approach towards stably integrating readily available low-level locomotion control and high-level planning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge