Explainable boosted linear regression for time series forecasting

Time series forecasting involves collecting and analyzing past observations to develop a model to extrapolate such observations into the future. Forecasting of future events is important in many fields to support decision making as it contributes to reducing the future uncertainty. We propose explainable boosted linear regression (EBLR) algorithm for time series forecasting, which is an iterative method that starts with a base model, and explains the model's errors through regression trees. At each iteration, the path leading to highest error is added as a new variable to the base model. In this regard, our approach can be considered as an improvement over general time series models since it enables incorporating nonlinear features by residuals explanation. More importantly, use of the single rule that contributes to the error most allows for interpretable results. The proposed approach extends to probabilistic forecasting through generating prediction intervals based on the empirical error distribution. We conduct a detailed numerical study with EBLR and compare against various other approaches. We observe that EBLR substantially improves the base model performance through extracted features, and provide a comparable performance to other well established approaches. The interpretability of the model predictions and high predictive accuracy of EBLR makes it a promising method for time series forecasting.

Evaluation of Local Explanation Methods for Multivariate Time Series Forecasting

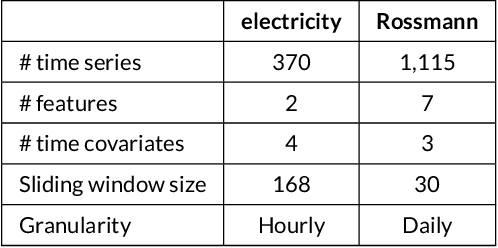
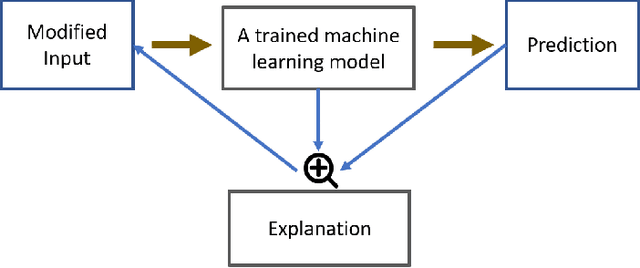
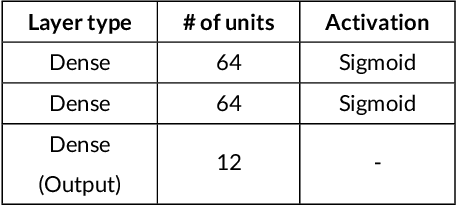
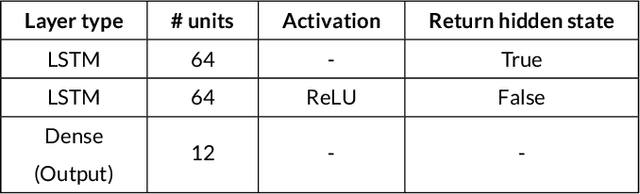
Being able to interpret a machine learning model is a crucial task in many applications of machine learning. Specifically, local interpretability is important in determining why a model makes particular predictions. Despite the recent focus on AI interpretability, there has been a lack of research in local interpretability methods for time series forecasting while the few interpretable methods that exist mainly focus on time series classification tasks. In this study, we propose two novel evaluation metrics for time series forecasting: Area Over the Perturbation Curve for Regression and Ablation Percentage Threshold. These two metrics can measure the local fidelity of local explanation models. We extend the theoretical foundation to collect experimental results on two popular datasets, \textit{Rossmann sales} and \textit{electricity}. Both metrics enable a comprehensive comparison of numerous local explanation models and find which metrics are more sensitive. Lastly, we provide heuristical reasoning for this analysis.