Hujie Pan
Weight Encode Reconstruction Network for Computed Tomography in a Semi-Case-Wise and Learning-Based Way
Oct 02, 2020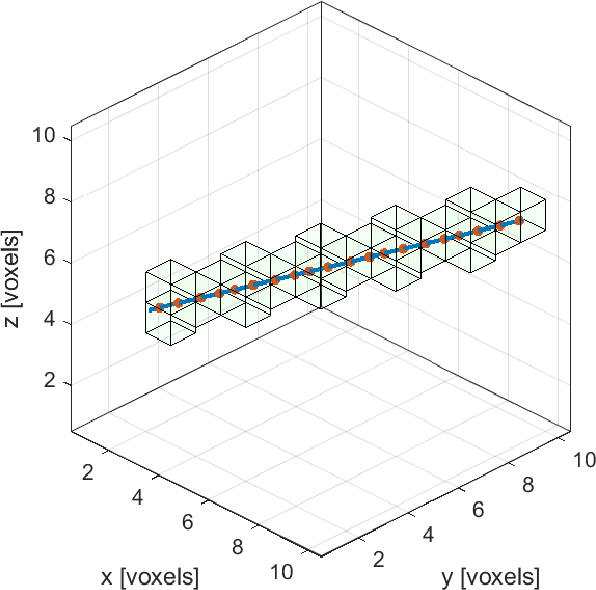
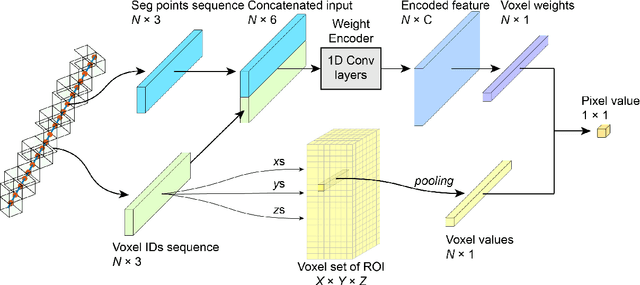

Abstract:Classic algebraic reconstruction technology (ART) for computed tomography requires pre-determined weights of the voxels for projecting pixel values. However, such weight cannot be accurately obtained due to the limitation of the physical understanding and computation resources. In this study, we propose a semi-case-wise learning-based method named Weight Encode Reconstruction Network (WERNet) to tackle the issues mentioned above. The model is trained in a self-supervised manner without the label of a voxel set. It contains two branches, including the voxel weight encoder and the voxel attention part. Using gradient normalization, we are able to co-train the encoder and voxel set numerically stably. With WERNet, the reconstructed result was obtained with a cosine similarity greater than 0.999 with the ground truth. Moreover, the model shows the extraordinary capability of denoising comparing to the classic ART method. In the generalization test of the model, the encoder is transferable from a voxel set with complex structure to the unseen cases without the deduction of the accuracy.
Towards Better Performance and More Explainable Uncertainty for 3D Object Detection of Autonomous Vehicles
Jun 22, 2020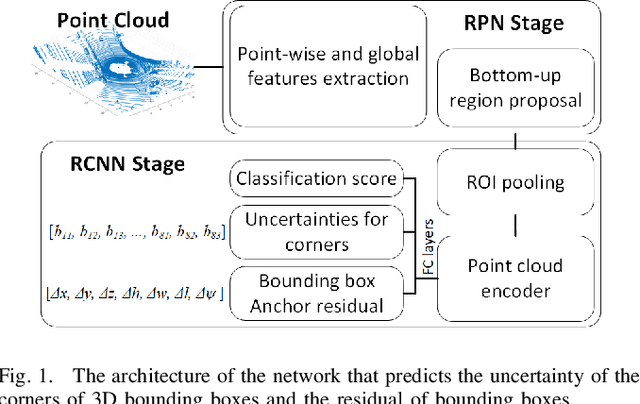
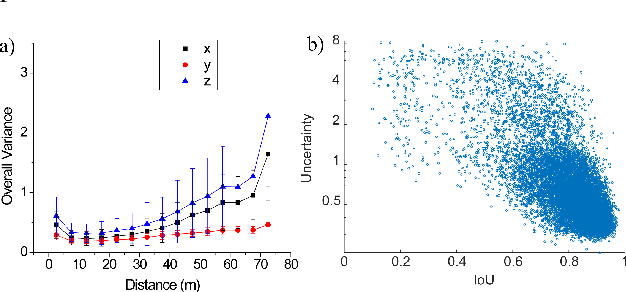
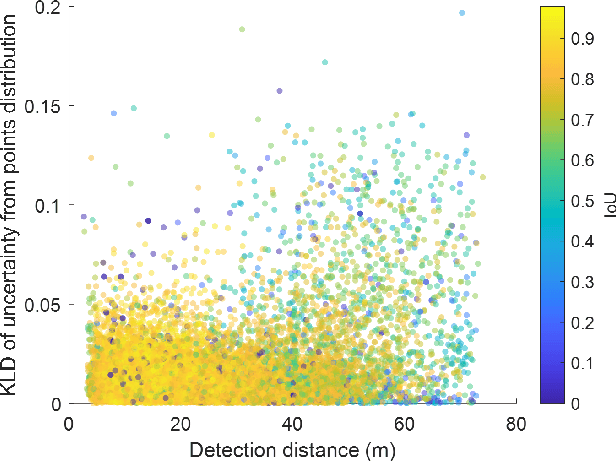
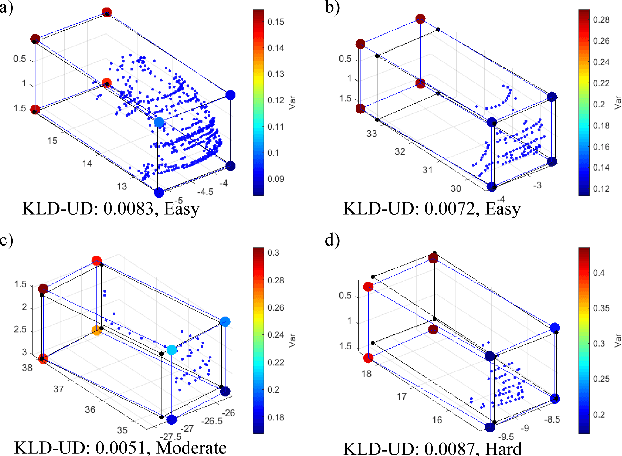
Abstract:In this paper, we propose a novel form of the loss function to increase the performance of LiDAR-based 3d object detection and obtain more explainable and convincing uncertainty for the prediction. The loss function was designed using corner transformation and uncertainty modeling. With the new loss function, the performance of our method on the val split of KITTI dataset shows up to a 15% increase in terms of Average Precision (AP) comparing with the baseline using simple L1 Loss. In the study of the characteristics of predicted uncertainties, we find that generally more accurate prediction of the bounding box is usually accompanied by lower uncertainty. The distribution of corner uncertainties agrees on the distribution of the point cloud in the bounding box, which means the corner with denser observed points has lower uncertainty. Moreover, our method also learns the constraint from the cuboid geometry of the bounding box in uncertainty prediction. Finally, we propose an efficient Bayesian updating method to recover the uncertainty for the original parameters of the bounding boxes which can help to provide probabilistic results for the planning module.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge