Utility-Probability Duality of Neural Networks

It is typically understood that the training of modern neural networks is a process of fitting the probability distribution of desired output. However, recent paradoxical observations in a number of language generation tasks let one wonder if this canonical probability-based explanation can really account for the empirical success of deep learning. To resolve this issue, we propose an alternative utility-based explanation to the standard supervised learning procedure in deep learning. The basic idea is to interpret the learned neural network not as a probability model but as an ordinal utility function that encodes the preference revealed in training data. In this perspective, training of the neural network corresponds to a utility learning process. Specifically, we show that for all neural networks with softmax outputs, the SGD learning dynamic of maximum likelihood estimation (MLE) can be seen as an iteration process that optimizes the neural network toward an optimal utility function. This utility-based interpretation can explain several otherwise-paradoxical observations about the neural networks thus trained. Moreover, our utility-based theory also entails an equation that can transform the learned utility values back to a new kind of probability estimation with which probability-compatible decision rules enjoy dramatic (double-digits) performance improvements. These evidences collectively reveal a phenomenon of utility-probability duality in terms of what modern neural networks are (truly) modeling: We thought they are one thing (probabilities), until the unexplainable showed up; changing mindset and treating them as another thing (utility values) largely reconcile the theory, despite remaining subtleties regarding its original (probabilistic) identity.

Lagrangian Method for Q-Function Learning (with Applications to Machine Translation)

This paper discusses a new approach to the fundamental problem of learning optimal Q-functions. In this approach, optimal Q-functions are formulated as saddle points of a nonlinear Lagrangian function derived from the classic Bellman optimality equation. The paper shows that the Lagrangian enjoys strong duality, in spite of its nonlinearity, which paves the way to a general Lagrangian method to Q-function learning. As a demonstration, the paper develops an imitation learning algorithm based on the duality theory, and applies the algorithm to a state-of-the-art machine translation benchmark. The paper then turns to demonstrate a symmetry breaking phenomenon regarding the optimality of the Lagrangian saddle points, which justifies a largely overlooked direction in developing the Lagrangian method.

Simpson's Bias in NLP Training

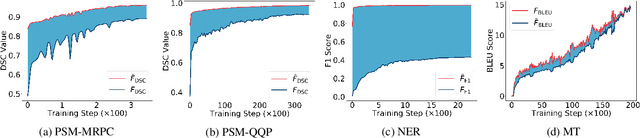
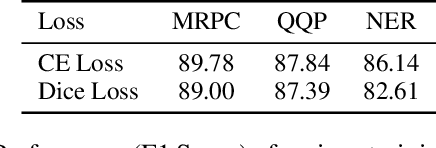
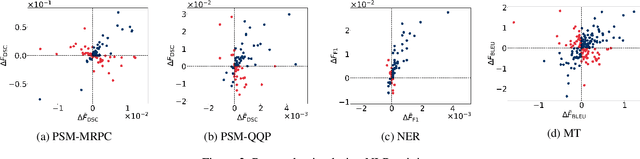
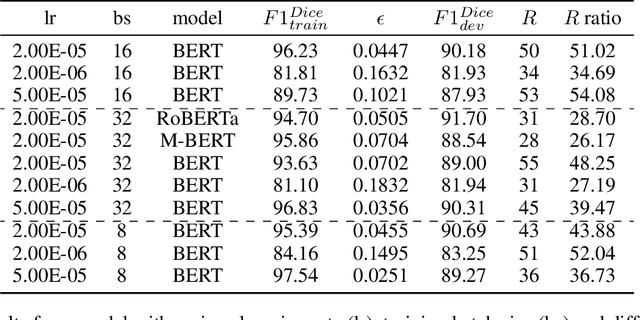
In most machine learning tasks, we evaluate a model $M$ on a given data population $S$ by measuring a population-level metric $F(S;M)$. Examples of such evaluation metric $F$ include precision/recall for (binary) recognition, the F1 score for multi-class classification, and the BLEU metric for language generation. On the other hand, the model $M$ is trained by optimizing a sample-level loss $G(S_t;M)$ at each learning step $t$, where $S_t$ is a subset of $S$ (a.k.a. the mini-batch). Popular choices of $G$ include cross-entropy loss, the Dice loss, and sentence-level BLEU scores. A fundamental assumption behind this paradigm is that the mean value of the sample-level loss $G$, if averaged over all possible samples, should effectively represent the population-level metric $F$ of the task, such as, that $\mathbb{E}[ G(S_t;M) ] \approx F(S;M)$. In this paper, we systematically investigate the above assumption in several NLP tasks. We show, both theoretically and experimentally, that some popular designs of the sample-level loss $G$ may be inconsistent with the true population-level metric $F$ of the task, so that models trained to optimize the former can be substantially sub-optimal to the latter, a phenomenon we call it, Simpson's bias, due to its deep connections with the classic paradox known as Simpson's reversal paradox in statistics and social sciences.

Steady State Analysis of Episodic Reinforcement Learning

This paper proves that the episodic learning environment of every finite-horizon decision task has a unique steady state under any behavior policy, and that the marginal distribution of the agent's input indeed approaches to the steady-state distribution in essentially all episodic learning processes. This observation supports an interestingly reversed mindset against conventional wisdom: While steady states are usually presumed to exist in continual learning and are considered less relevant in episodic learning, it turns out they are guaranteed to exist for the latter. Based on this insight, the paper further develops connections between episodic and continual RL for several important concepts that have been separately treated in the two RL formalisms. Practically, the existence of unique and approachable steady state enables a general, reliable, and efficient way to collect data in episodic RL tasks, which the paper applies to policy gradient algorithms as a demonstration, based on a new steady-state policy gradient theorem. The paper also proposes and empirically evaluates a perturbation method that facilitates rapid mixing in real-world tasks.