Simpson's Bias in NLP Training
Paper and Code
Mar 13, 2021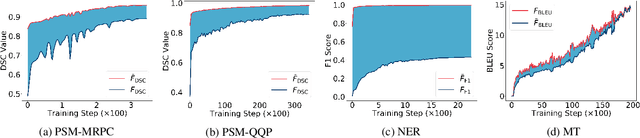
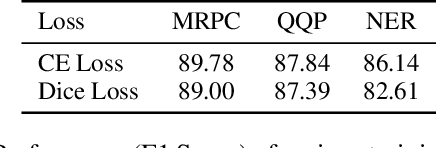
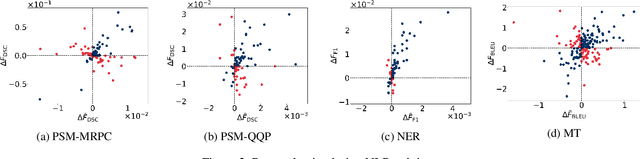
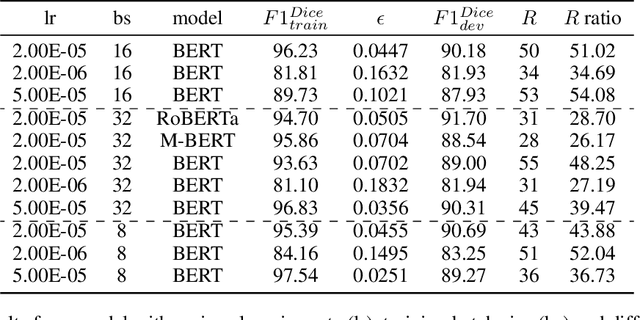
In most machine learning tasks, we evaluate a model $M$ on a given data population $S$ by measuring a population-level metric $F(S;M)$. Examples of such evaluation metric $F$ include precision/recall for (binary) recognition, the F1 score for multi-class classification, and the BLEU metric for language generation. On the other hand, the model $M$ is trained by optimizing a sample-level loss $G(S_t;M)$ at each learning step $t$, where $S_t$ is a subset of $S$ (a.k.a. the mini-batch). Popular choices of $G$ include cross-entropy loss, the Dice loss, and sentence-level BLEU scores. A fundamental assumption behind this paradigm is that the mean value of the sample-level loss $G$, if averaged over all possible samples, should effectively represent the population-level metric $F$ of the task, such as, that $\mathbb{E}[ G(S_t;M) ] \approx F(S;M)$. In this paper, we systematically investigate the above assumption in several NLP tasks. We show, both theoretically and experimentally, that some popular designs of the sample-level loss $G$ may be inconsistent with the true population-level metric $F$ of the task, so that models trained to optimize the former can be substantially sub-optimal to the latter, a phenomenon we call it, Simpson's bias, due to its deep connections with the classic paradox known as Simpson's reversal paradox in statistics and social sciences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge