Stability of Random Forests and Coverage of Random-Forest Prediction Intervals

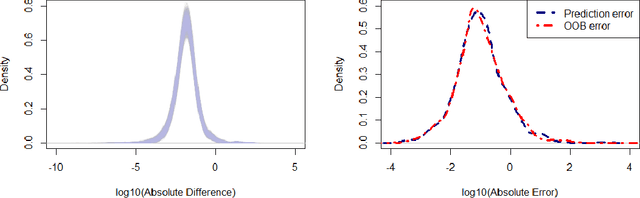
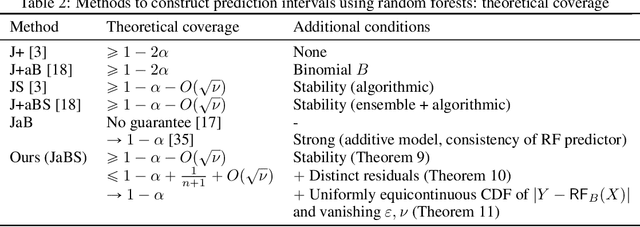
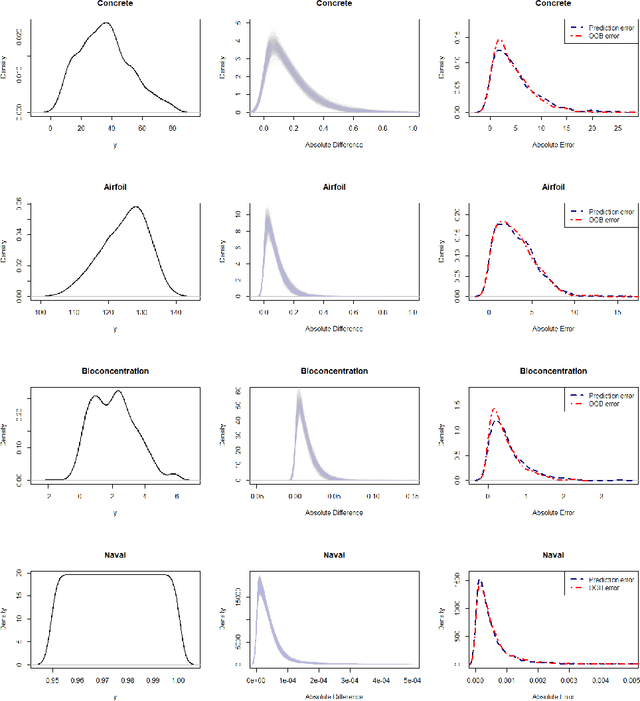
We establish stability of random forests under the mild condition that the squared response ($Y^2$) does not have a heavy tail. In particular, our analysis holds for the practical version of random forests that is implemented in popular packages like \texttt{randomForest} in \texttt{R}. Empirical results show that stability may persist even beyond our assumption and hold for heavy-tailed $Y^2$. Using the stability property, we prove a non-asymptotic lower bound for the coverage probability of prediction intervals constructed from the out-of-bag error of random forests. With another mild condition that is typically satisfied when $Y$ is continuous, we also establish a complementary upper bound, which can be similarly established for the jackknife prediction interval constructed from an arbitrary stable algorithm. We also discuss the asymptotic coverage probability under assumptions weaker than those considered in previous literature. Our work implies that random forests, with its stability property, is an effective machine learning method that can provide not only satisfactory point prediction but also justified interval prediction at almost no extra computational cost.

Structure Learning in Bayesian Networks of Moderate Size by Efficient Sampling

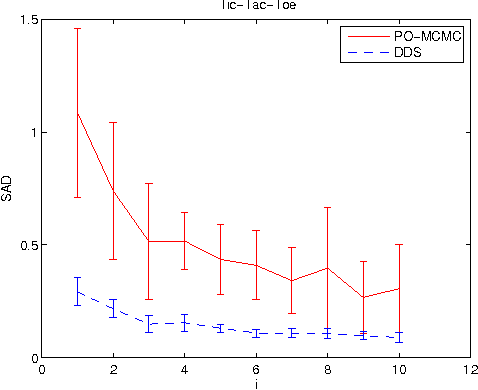
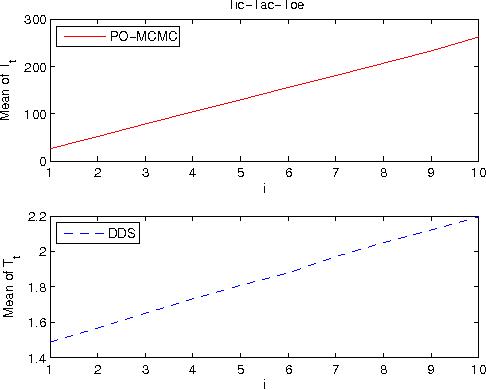
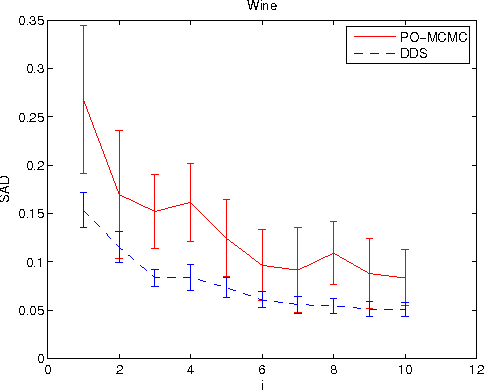
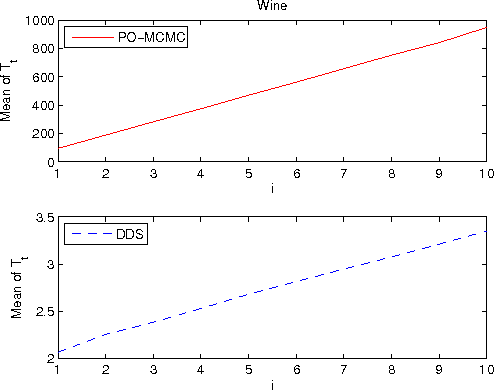
We study the Bayesian model averaging approach to learning Bayesian network structures (DAGs) from data. We develop new algorithms including the first algorithm that is able to efficiently sample DAGs according to the exact structure posterior. The DAG samples can then be used to construct estimators for the posterior of any feature. We theoretically prove good properties of our estimators and empirically show that our estimators considerably outperform the estimators from the previous state-of-the-art methods.