Robotic Control Optimization Through Kernel Selection in Safe Bayesian Optimization

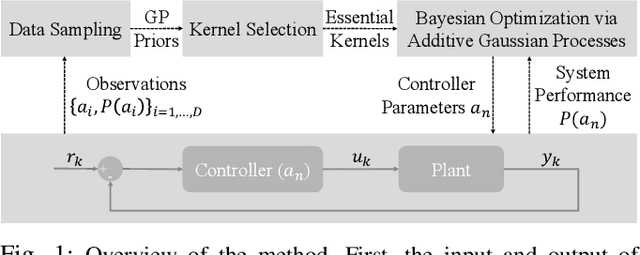
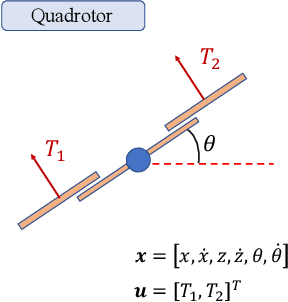
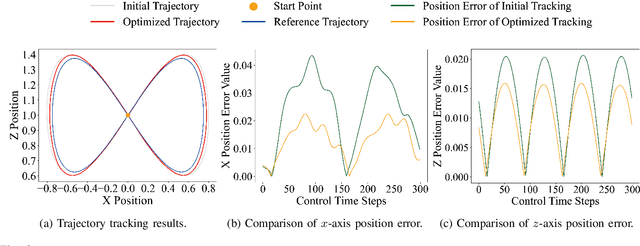
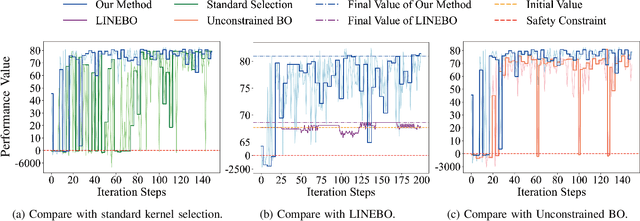
Control system optimization has long been a fundamental challenge in robotics. While recent advancements have led to the development of control algorithms that leverage learning-based approaches, such as SafeOpt, to optimize single feedback controllers, scaling these methods to high-dimensional complex systems with multiple controllers remains an open problem. In this paper, we propose a novel learning-based control optimization method, which enhances the additive Gaussian process-based Safe Bayesian Optimization algorithm to efficiently tackle high-dimensional problems through kernel selection. We use PID controller optimization in drones as a representative example and test the method on Safe Control Gym, a benchmark designed for evaluating safe control techniques. We show that the proposed method provides a more efficient and optimal solution for high-dimensional control optimization problems, demonstrating significant improvements over existing techniques.

Safe Bayesian Optimization for High-Dimensional Control Systems via Additive Gaussian Processes

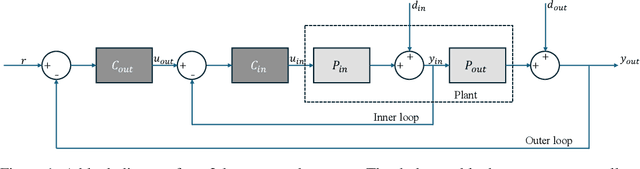
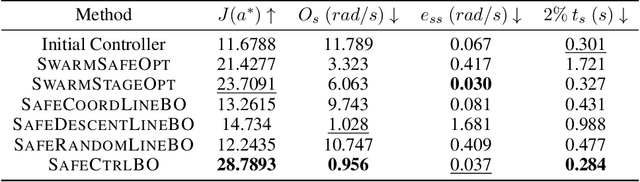
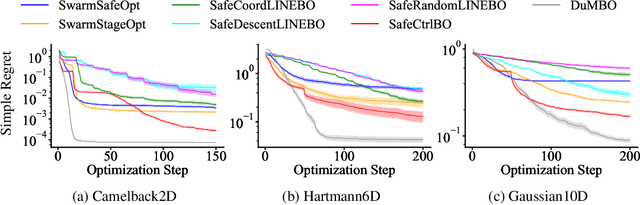
Controller tuning and optimization have been among the most fundamental problems in robotics and mechatronic systems. The traditional methodology is usually model-based, but its performance heavily relies on an accurate mathematical model of the system. In control applications with complex dynamics, obtaining a precise model is often challenging, leading us towards a data-driven approach. While optimizing a single controller has been explored by various researchers, it remains a challenge to obtain the optimal controller parameters safely and efficiently when multiple controllers are involved. In this paper, we propose a high-dimensional safe Bayesian optimization method based on additive Gaussian processes to optimize multiple controllers simultaneously and safely. Additive Gaussian kernels replace the traditional squared-exponential kernels or Mat\'ern kernels, enhancing the efficiency with which Gaussian processes update information on unknown functions. Experimental results on a permanent magnet synchronous motor (PMSM) demonstrate that compared to existing safe Bayesian optimization algorithms, our method can obtain optimal parameters more efficiently while ensuring safety.