Hongxiao Li
KAIROS: Unified Training for Universal Non-Autoregressive Time Series Forecasting
Oct 02, 2025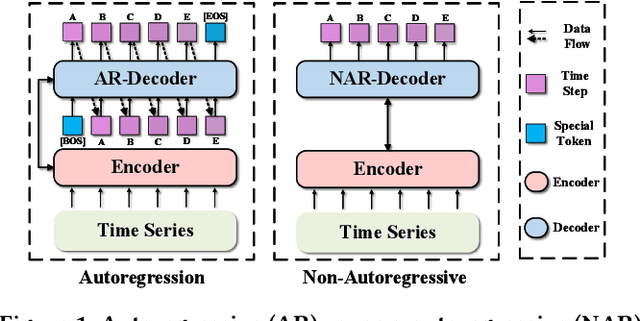

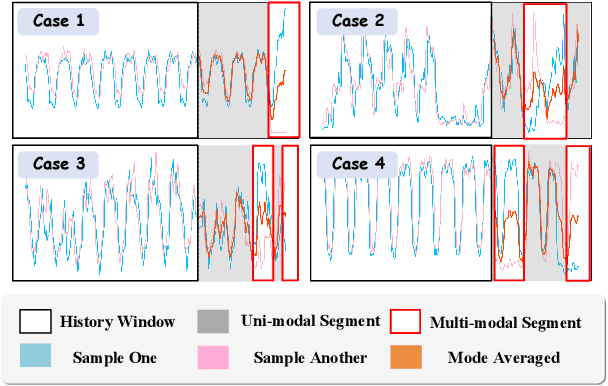
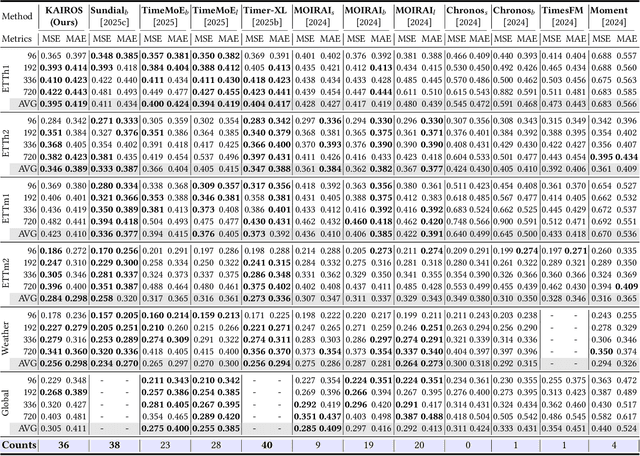
Abstract:In the World Wide Web, reliable time series forecasts provide the forward-looking signals that drive resource planning, cache placement, and anomaly response, enabling platforms to operate efficiently as user behavior and content distributions evolve. Compared with other domains, time series forecasting for Web applications requires much faster responsiveness to support real-time decision making. We present KAIROS, a non-autoregressive time series forecasting framework that directly models segment-level multi-peak distributions. Unlike autoregressive approaches, KAIROS avoids error accumulation and achieves just-in-time inference, while improving over existing non-autoregressive models that collapse to over-smoothed predictions. Trained on the large-scale corpus, KAIROS demonstrates strong zero-shot generalization on six widely used benchmarks, delivering forecasting performance comparable to state-of-the-art foundation models with similar scale, at a fraction of their inference cost. Beyond empirical results, KAIROS highlights the importance of non-autoregressive design as a scalable paradigm for foundation models in time series.
IterLara: A Turing Complete Algebra for Big Data, AI, Scientific Computing, and Database
Jul 17, 2023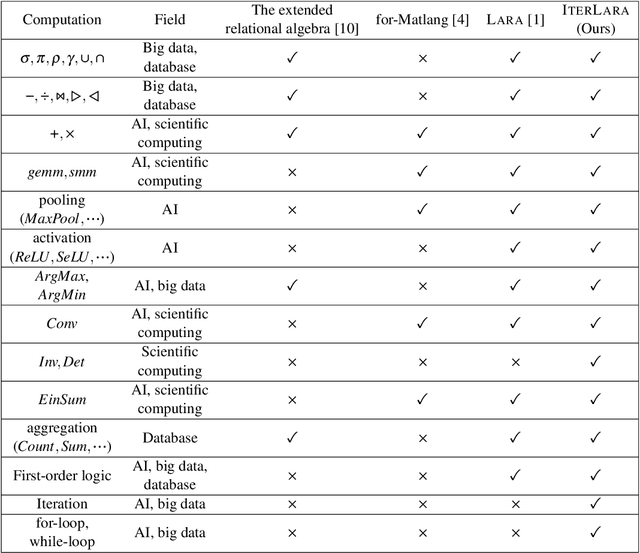
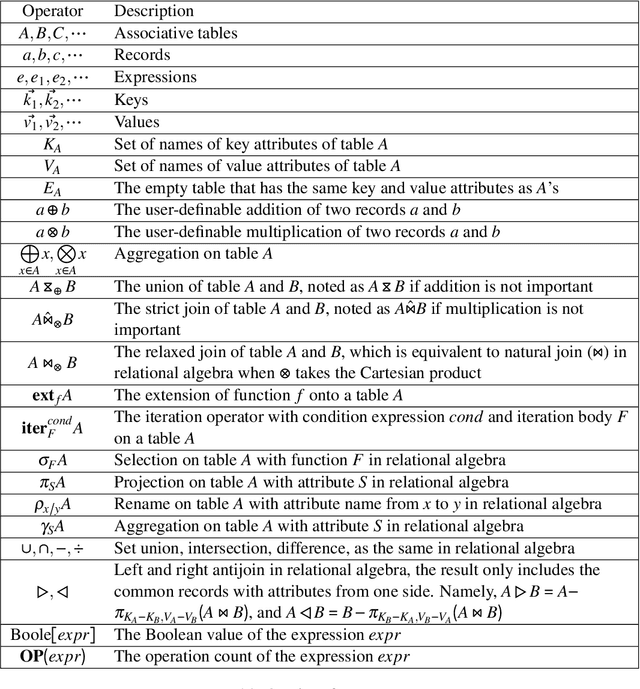
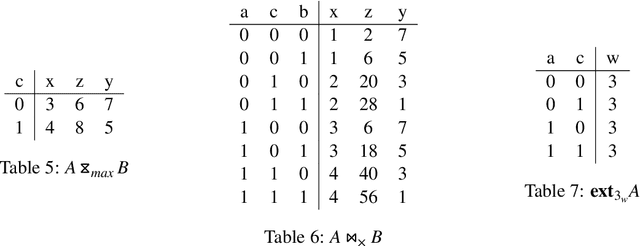
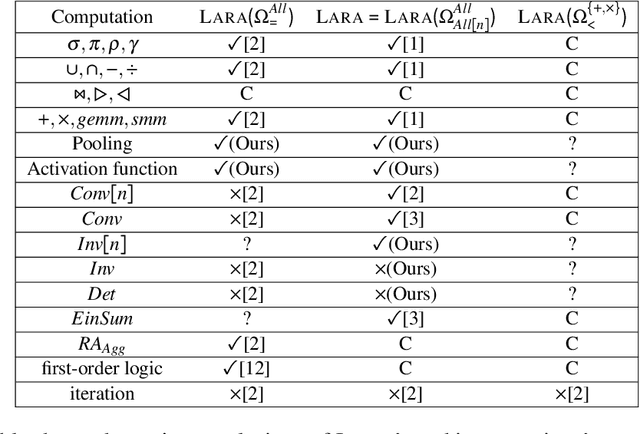
Abstract:\textsc{Lara} is a key-value algebra that aims at unifying linear and relational algebra with three types of operation abstraction. The study of \textsc{Lara}'s expressive ability reports that it can represent relational algebra and most linear algebra operations. However, several essential computations, such as matrix inversion and determinant, cannot be expressed in \textsc{Lara}. \textsc{Lara} cannot represent global and iterative computation, either. This article proposes \textsc{IterLara}, extending \textsc{Lara} with iterative operators, to provide an algebraic model that unifies operations in general-purpose computing, like big data, AI, scientific computing, and database. We study the expressive ability of \textsc{Lara} and \textsc{IterLara} and prove that \textsc{IterLara} with aggregation functions can represent matrix inversion, determinant. Besides, we demonstrate that \textsc{IterLara} with no limitation of function utility is Turing complete. We also propose the Operation Count (OP) as a metric of computation amount for \textsc{IterLara} and ensure that the OP metric is in accordance with the existing computation metrics.
ToL: A Tensor of List-Based Unified Computation Model
Dec 21, 2022
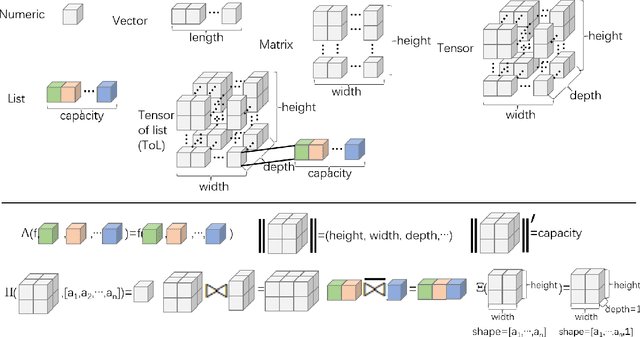


Abstract:Previous computation models either have equivalent abilities in representing all computations but fail to provide primitive operators for programming complex algorithms or lack generalized expression ability to represent newly-added computations. This article presents a unified computation model with generalized expression ability and a concise set of primitive operators for programming high-level algorithms. We propose a unified data abstraction -- Tensor of List, and offer a unified computation model based on Tensor of List, which we call the ToL model (in short, ToL). ToL introduces five atomic computations that can represent any elementary computation by finite composition, ensured with strict formal proof. Based on ToL, we design a pure-functional language -- ToLang. ToLang provides a concise set of primitive operators that can be used to program complex big data and AI algorithms. Our evaluations show ToL has generalized expression ability and a built-in performance indicator, born with a strictly defined computation metric -- elementary operation count (EOPs), consistent with FLOPs within a small error range.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge