IterLara: A Turing Complete Algebra for Big Data, AI, Scientific Computing, and Database
Paper and Code
Jul 17, 2023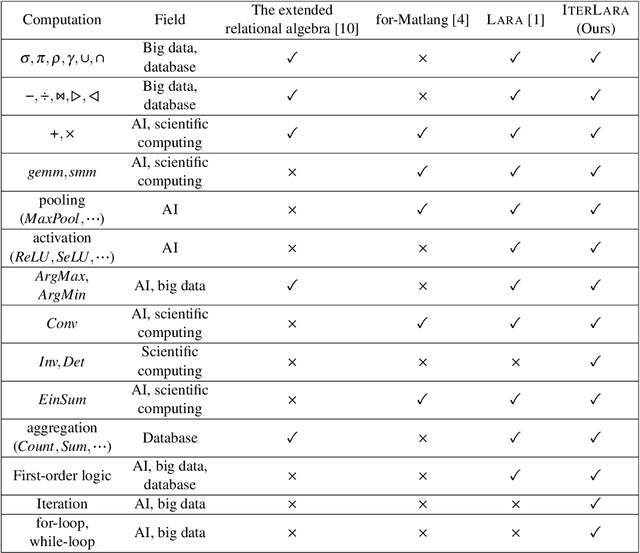
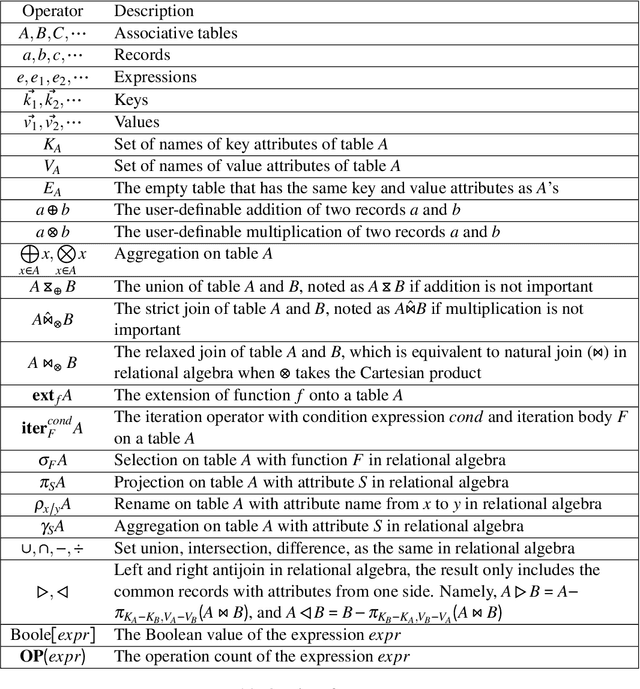
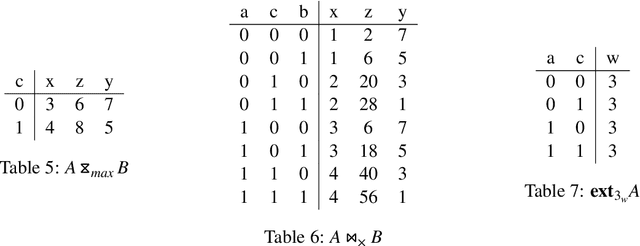
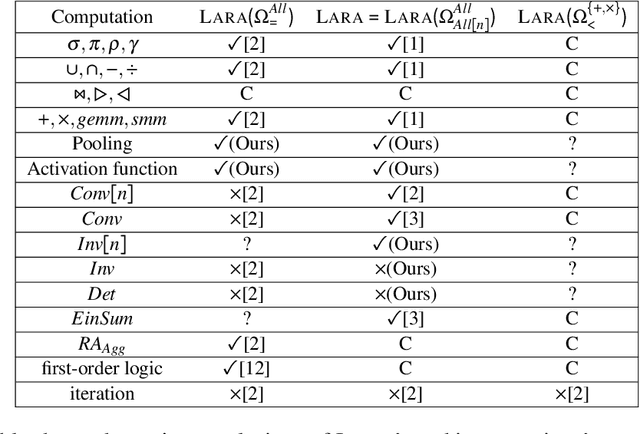
\textsc{Lara} is a key-value algebra that aims at unifying linear and relational algebra with three types of operation abstraction. The study of \textsc{Lara}'s expressive ability reports that it can represent relational algebra and most linear algebra operations. However, several essential computations, such as matrix inversion and determinant, cannot be expressed in \textsc{Lara}. \textsc{Lara} cannot represent global and iterative computation, either. This article proposes \textsc{IterLara}, extending \textsc{Lara} with iterative operators, to provide an algebraic model that unifies operations in general-purpose computing, like big data, AI, scientific computing, and database. We study the expressive ability of \textsc{Lara} and \textsc{IterLara} and prove that \textsc{IterLara} with aggregation functions can represent matrix inversion, determinant. Besides, we demonstrate that \textsc{IterLara} with no limitation of function utility is Turing complete. We also propose the Operation Count (OP) as a metric of computation amount for \textsc{IterLara} and ensure that the OP metric is in accordance with the existing computation metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge