Future Predictive Success-or-Failure Classification for Long-Horizon Robotic Tasks

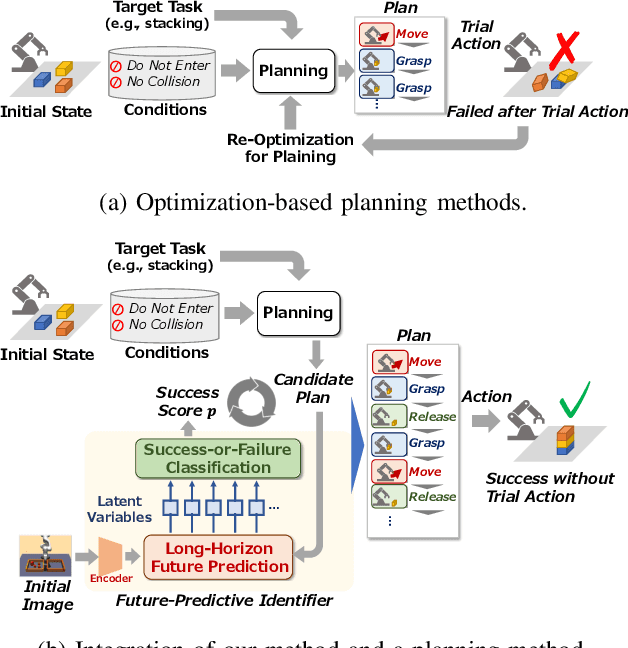
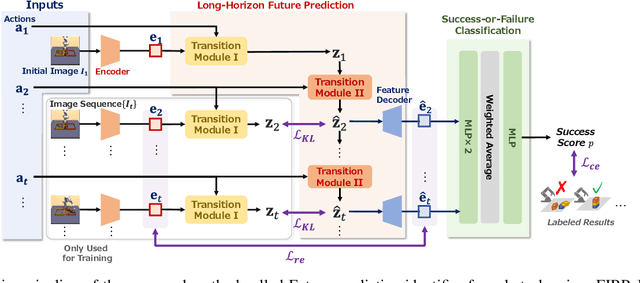
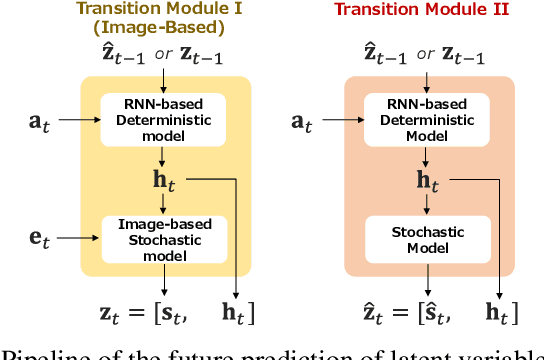
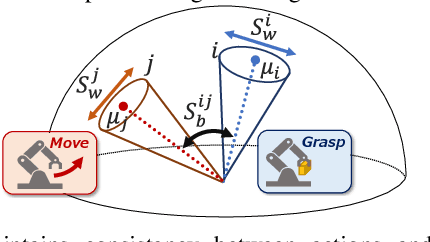
Automating long-horizon tasks with a robotic arm has been a central research topic in robotics. Optimization-based action planning is an efficient approach for creating an action plan to complete a given task. Construction of a reliable planning method requires a design process of conditions, e.g., to avoid collision between objects. The design process, however, has two critical issues: 1) iterative trials--the design process is time-consuming due to the trial-and-error process of modifying conditions, and 2) manual redesign--it is difficult to cover all the necessary conditions manually. To tackle these issues, this paper proposes a future-predictive success-or-failure-classification method to obtain conditions automatically. The key idea behind the proposed method is an end-to-end approach for determining whether the action plan can complete a given task instead of manually redesigning the conditions. The proposed method uses a long-horizon future-prediction method to enable success-or-failure classification without the execution of an action plan. This paper also proposes a regularization term called transition consistency regularization to provide easy-to-predict feature distribution. The regularization term improves future prediction and classification performance. The effectiveness of our method is demonstrated through classification and robotic-manipulation experiments.

Fast MILP-based Task and Motion Planning for Pick-and-Place with Hard/Soft Constraints of Collision-Free Route

We present new models of optimization-based task and motion planning (TAMP) for robotic pick-and-place (P&P), which plan action sequences and motion trajectory with low computational costs. We improved an existing state-of-the-art TAMP model integrated with the collision avoidance, which is formulated as a mixed-integer linear programing (MILP) problem. To enable the MILP solver to search for solutions efficiently, we introduced two approaches leveraging features of collision avoidance in robotic P&P. The first approach reduces number of binary variables, which is related to the collision avoidance of delivery objects, by reformulating them as continuous variables with additional hard constraints. These hard constraints maintain consistency by conditionally propagating binary values, which is related to the carry action state and collision avoidance of robots, to the reformulated continuous variables. The second approach is more aware of the branch-and-bound method, which is the fundamental algorithm of modern MILP solvers. This approach guides the MILP solver to find integer solutions with shallower branching by adding a soft constraint, which softly restricts a robot's routes around delivery objects. We demonstrate the effectiveness of the proposed models with a modern MILP solver.