Spatial-photonic Boltzmann machines: low-rank combinatorial optimization and statistical learning by spatial light modulation

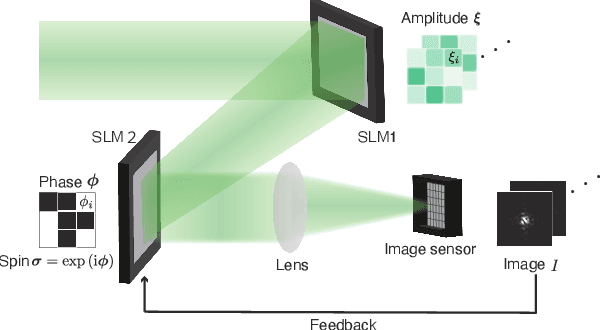
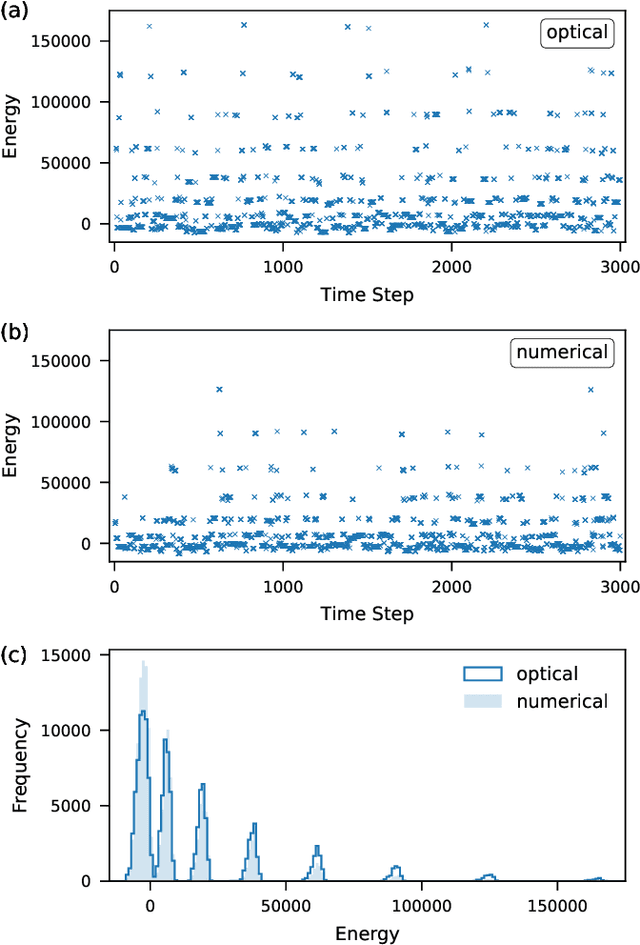
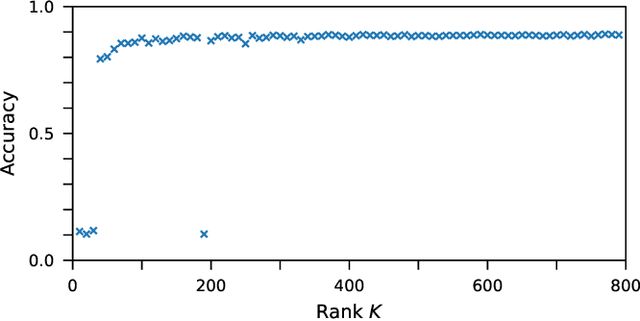
The spatial-photonic Ising machine (SPIM) [D. Pierangeli et al., Phys. Rev. Lett. 122, 213902 (2019)] is a promising optical architecture utilizing spatial light modulation for solving large-scale combinatorial optimization problems efficiently. However, the SPIM can accommodate Ising problems with only rank-one interaction matrices, which limits its applicability to various real-world problems. In this Letter, we propose a new computing model for the SPIM that can accommodate any Ising problem without changing its optical implementation. The proposed model is particularly efficient for Ising problems with low-rank interaction matrices, such as knapsack problems. Moreover, the model acquires learning ability and can thus be termed a spatial-photonic Boltzmann machine (SPBM). We demonstrate that learning, classification, and sampling of the MNIST handwritten digit images are achieved efficiently using SPBMs with low-rank interactions. Thus, the proposed SPBM model exhibits higher practical applicability to various problems of combinatorial optimization and statistical learning, without losing the scalability inherent in the SPIM architecture.

Entropic Herding

Herding is a deterministic algorithm used to generate data points that can be regarded as random samples satisfying input moment conditions. The algorithm is based on the complex behavior of a high-dimensional dynamical system and is inspired by the maximum entropy principle of statistical inference. In this paper, we propose an extension of the herding algorithm, called entropic herding, which generates a sequence of distributions instead of points. Entropic herding is derived as the optimization of the target function obtained from the maximum entropy principle. Using the proposed entropic herding algorithm as a framework, we discuss a closer connection between herding and the maximum entropy principle. Specifically, we interpret the original herding algorithm as a tractable version of entropic herding, the ideal output distribution of which is mathematically represented. We further discuss how the complex behavior of the herding algorithm contributes to optimization. We argue that the proposed entropic herding algorithm extends the application of herding to probabilistic modeling. In contrast to original herding, entropic herding can generate a smooth distribution such that both efficient probability density calculation and sample generation become possible. To demonstrate the viability of these arguments in this study, numerical experiments were conducted, including a comparison with other conventional methods, on both synthetic and real data.

Extended dynamic mode decomposition with dictionary learning using neural ordinary differential equations

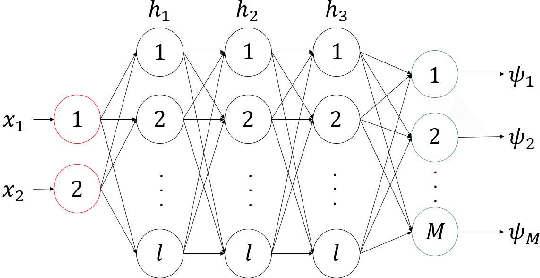
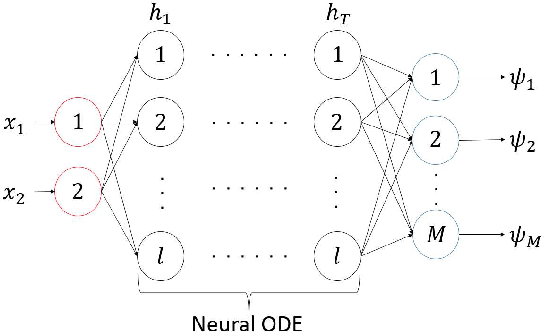
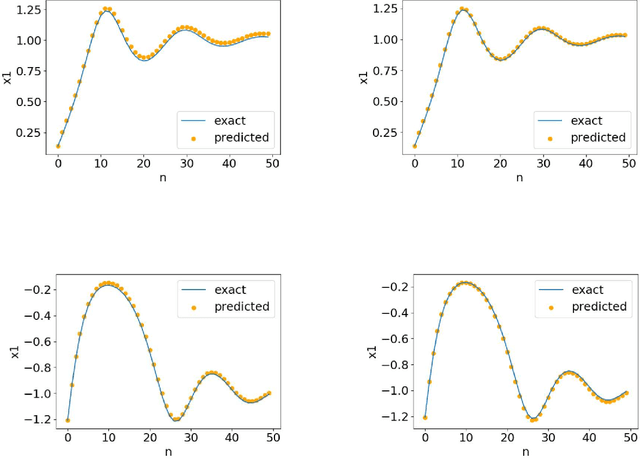
Nonlinear phenomena can be analyzed via linear techniques using operator-theoretic approaches. Data-driven method called the extended dynamic mode decomposition (EDMD) and its variants, which approximate the Koopman operator associated with the nonlinear phenomena, have been rapidly developing by incorporating machine learning methods. Neural ordinary differential equations (NODEs), which are a neural network equipped with a continuum of layers, and have high parameter and memory efficiencies, have been proposed. In this paper, we propose an algorithm to perform EDMD using NODEs. NODEs are used to find a parameter-efficient dictionary which provides a good finite-dimensional approximation of the Koopman operator. We show the superiority of the parameter efficiency of the proposed method through numerical experiments.

Hypergraph $p$-Laplacian: A Differential Geometry View

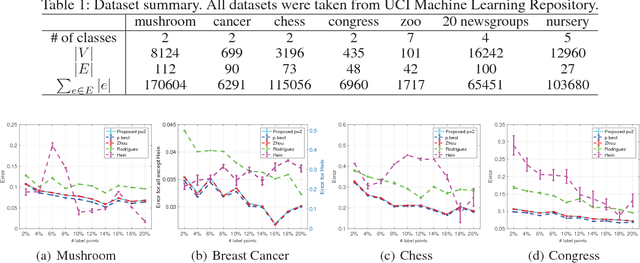
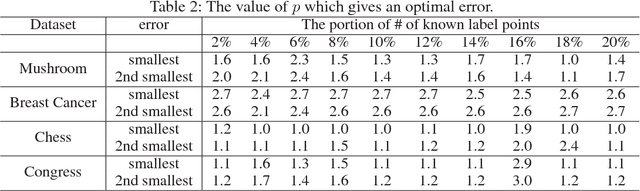
The graph Laplacian plays key roles in information processing of relational data, and has analogies with the Laplacian in differential geometry. In this paper, we generalize the analogy between graph Laplacian and differential geometry to the hypergraph setting, and propose a novel hypergraph $p$-Laplacian. Unlike the existing two-node graph Laplacians, this generalization makes it possible to analyze hypergraphs, where the edges are allowed to connect any number of nodes. Moreover, we propose a semi-supervised learning method based on the proposed hypergraph $p$-Laplacian, and formalize them as the analogue to the Dirichlet problem, which often appears in physics. We further explore theoretical connections to normalized hypergraph cut on a hypergraph, and propose normalized cut corresponding to hypergraph $p$-Laplacian. The proposed $p$-Laplacian is shown to outperform standard hypergraph Laplacians in the experiment on a hypergraph semi-supervised learning and normalized cut setting.