Hypergraph $p$-Laplacian: A Differential Geometry View
Paper and Code
Nov 22, 2017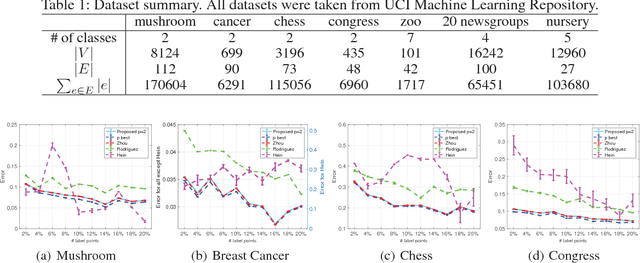
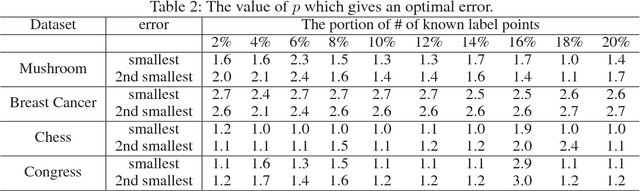

The graph Laplacian plays key roles in information processing of relational data, and has analogies with the Laplacian in differential geometry. In this paper, we generalize the analogy between graph Laplacian and differential geometry to the hypergraph setting, and propose a novel hypergraph $p$-Laplacian. Unlike the existing two-node graph Laplacians, this generalization makes it possible to analyze hypergraphs, where the edges are allowed to connect any number of nodes. Moreover, we propose a semi-supervised learning method based on the proposed hypergraph $p$-Laplacian, and formalize them as the analogue to the Dirichlet problem, which often appears in physics. We further explore theoretical connections to normalized hypergraph cut on a hypergraph, and propose normalized cut corresponding to hypergraph $p$-Laplacian. The proposed $p$-Laplacian is shown to outperform standard hypergraph Laplacians in the experiment on a hypergraph semi-supervised learning and normalized cut setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge