DeePoly: A High-Order Accuracy and Efficiency Deep-Polynomial Framework for Scientific Machine Learning

Recently, machine learning methods have gained significant traction in scientific computing, particularly for solving Partial Differential Equations (PDEs). However, methods based on deep neural networks (DNNs) often lack convergence guarantees and computational efficiency compared to traditional numerical schemes. This work introduces DeePoly, a novel framework that transforms the solution paradigm from pure non-convex parameter optimization to a two-stage approach: first employing a DNN to capture complex global features, followed by linear space optimization with combined DNN-extracted features (Scoper) and polynomial basis functions (Sniper). This strategic combination leverages the complementary strengths of both methods -- DNNs excel at approximating complex global features (i.e., high-gradient features) and stabilize the polynomial approximation while polynomial bases provide high-precision local corrections with convergence guarantees. Theoretical analysis and numerical experiments demonstrate that this approach significantly enhances both high-order accuracy and efficiency across diverse problem types while maintaining mesh-free and scheme-free properties. This paper also serves as a theoretical exposition for the open-source project DeePoly.

A general physics-constrained method for the modelling of equation's closure terms with sparse data

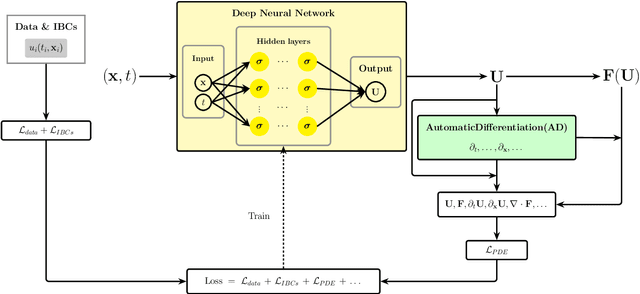
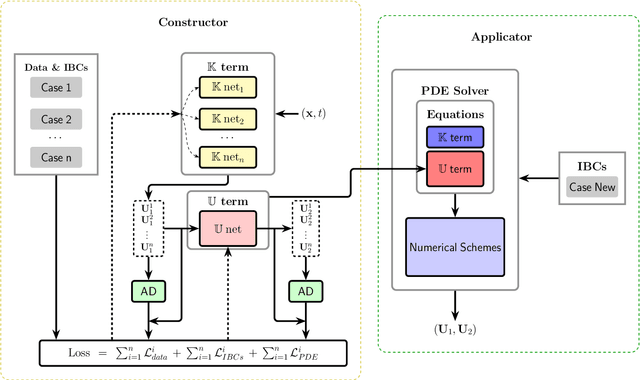
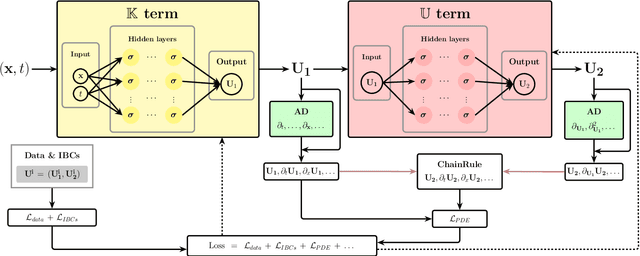
Accurate modeling of closure terms is a critical challenge in engineering and scientific research, particularly when data is sparse (scarse or incomplete), making widely applicable models difficult to develop. This study proposes a novel approach for constructing closure models in such challenging scenarios. We introduce a Series-Parallel Multi-Network Architecture that integrates Physics-Informed Neural Networks (PINNs) to incorporate physical constraints and heterogeneous data from multiple initial and boundary conditions, while employing dedicated subnetworks to independently model unknown closure terms, enhancing generalizability across diverse problems. These closure models are integrated into an accurate Partial Differential Equation (PDE) solver, enabling robust solutions to complex predictive simulations in engineering applications.

Numerical Approximation Capacity of Neural Networks with Bounded Parameters: Do Limits Exist, and How Can They Be Measured?

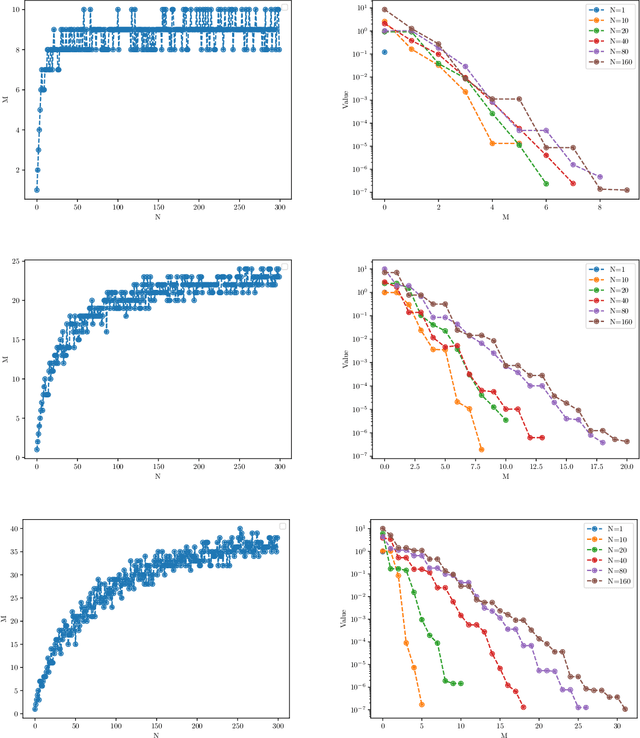
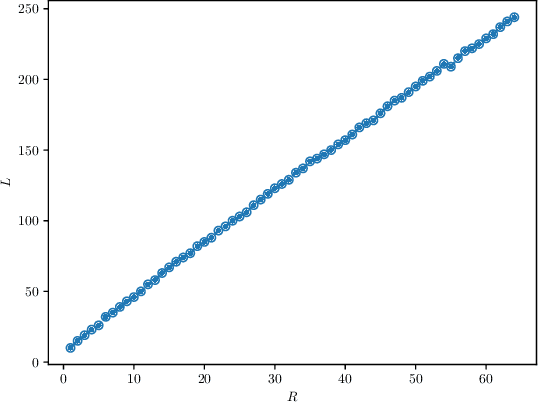
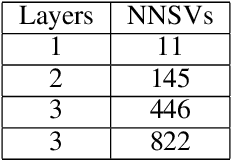
The Universal Approximation Theorem posits that neural networks can theoretically possess unlimited approximation capacity with a suitable activation function and a freely chosen or trained set of parameters. However, a more practical scenario arises when these neural parameters, especially the nonlinear weights and biases, are bounded. This leads us to question: \textbf{Does the approximation capacity of a neural network remain universal, or does it have a limit when the parameters are practically bounded? And if it has a limit, how can it be measured?} Our theoretical study indicates that while universal approximation is theoretically feasible, in practical numerical scenarios, Deep Neural Networks (DNNs) with any analytic activation functions (such as Tanh and Sigmoid) can only be approximated by a finite-dimensional vector space under a bounded nonlinear parameter space (NP space), whether in a continuous or discrete sense. Based on this study, we introduce the concepts of \textit{$\epsilon$ outer measure} and \textit{Numerical Span Dimension (NSdim)} to quantify the approximation capacity limit of a family of networks both theoretically and practically. Furthermore, drawing on our new theoretical study and adopting a fresh perspective, we strive to understand the relationship between back-propagation neural networks and random parameter networks (such as the Extreme Learning Machine (ELM)) with both finite and infinite width. We also aim to provide fresh insights into regularization, the trade-off between width and depth, parameter space, width redundancy, condensation, and other related important issues.