Information flow and Laplacian dynamics on local optima networks

We propose a new way of looking at local optima networks (LONs). LONs represent fitness landscapes; the nodes are local optima, and the edges are search transitions between them. Many metrics computed on LONs have been proposed and shown to be linked to metaheuristic search difficulty. These have typically considered LONs as describing static structures. In contrast to this, Laplacian dynamics (LD) is an approach to consider the information flow across a network as a dynamical process. We adapt and apply LD to the context of LONs. As a testbed, we consider instances from the quadratic assignment problem (QAP) library. Metrics related to LD are proposed and these are compared with existing LON metrics. The results show that certain LD metrics are strong predictors of metaheuristic performance for iterated local search and tabu search.

Do Random and Chaotic Sequences Really Cause Different PSO Performance? Further Results

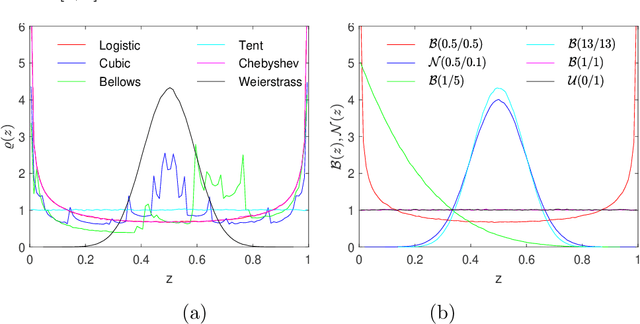
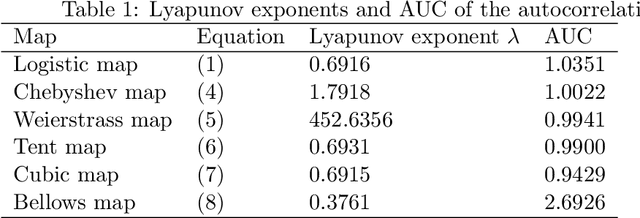
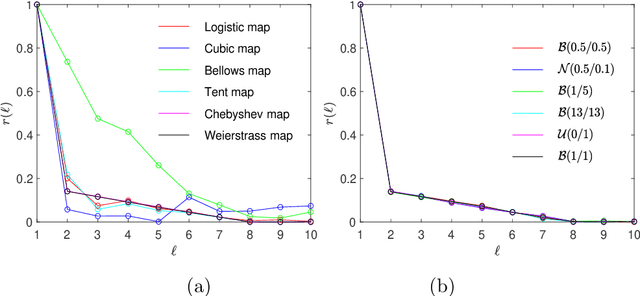
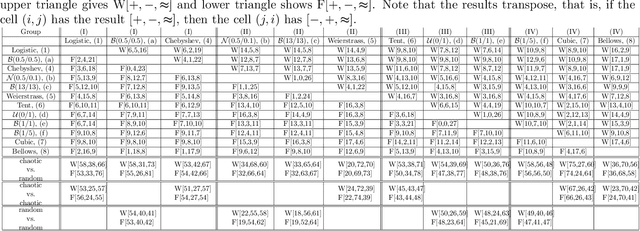
Empirical results show that PSO performance may be different if using either chaotic or random sequences to drive the algorithm's search dynamics. We analyze the phenomenon by evaluating the performance based on a benchmark of test functions and comparing random and chaotic sequences according to equality or difference in underlying distribution or density. Our results show that the underlying distribution is the main influential factor in performance and thus the assumption of general and systematic performance differences between chaos and random appears not plausible.

Wrong Colored Vermeer: Color-Symmetric Image Distortion

Color symmetry implies that the colors of geometrical objects are assigned according to their symmetry properties. It is defined by associating the elements of the symmetry group with a color permutation. I use this concept for generative art and apply symmetry-consistent color distortions to images of paintings by Johannes Vermeer. The color permutations are realized as mappings of the HSV color space onto itself.

Designing color symmetry in stigmergic art

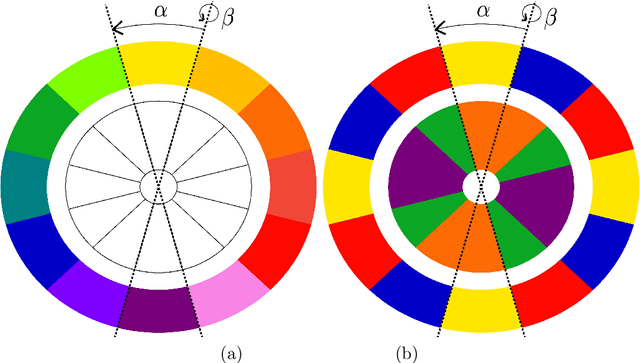
Color symmetry is an extension of symmetry imposed by isometric transformations and means that the colors of geometrical objects are assigned according to the symmetry properties of the objects. A color symmetry permutes the coloring of the objects consistently with their symmetry group. We apply this concept to bio-inspired generative art. Therefore, we interpret the geometrical objects as motifs that may repeat themselves with a symmetry-consistent coloring. The motifs are obtained by design principles from stigmergy. We discuss a design procedure and present visual results.

Constructing transient amplifiers for death-Birth updating: A case study of cubic and quartic regular graphs

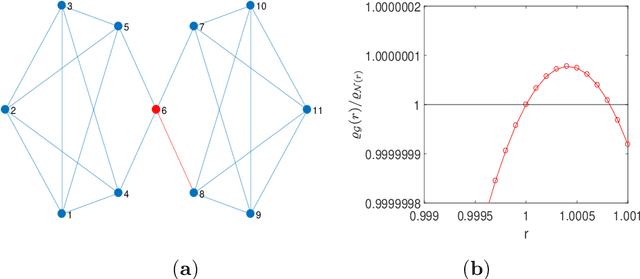
A central question of evolutionary dynamics on graphs is whether or not a mutation introduced in a population of residents survives and eventually even spreads to the whole population, or gets extinct. The outcome naturally depends on the fitness of the mutant and the rules by which mutants and residents may propagate on the network, but arguably the most determining factor is the network structure. Some structured networks are transient amplifiers. They increase for a certain fitness range the fixation probability of beneficial mutations as compared to a well-mixed population. We study a perturbation methods for identifying transient amplifiers for death-Birth updating. The method includes calculating the coalescence times of random walks on graphs and finding the vertex with the largest remeeting time. If the graph is perturbed by removing an edge from this vertex, there is a certain likelihood that the resulting perturbed graph is a transient amplifier. We test all pairwise nonisomorphic cubic and quartic regular graphs up to a certain size and thus cover the whole structural range expressible by these graphs. We carry out a spectral analysis and show that the graphs from which the transient amplifiers can be constructed share certain structural properties. The graphs are path-like, have low conductance and are rather easy to divide into subgraphs by removing edges and/or vertices. This is connected with the subgraphs being identical (or almost identical) building blocks and the frequent occurrence of cut and/or hinge vertices. Identifying spectral and structural properties may promote finding and designing such networks.

Convergence analysis of particle swarm optimization using stochastic Lyapunov functions and quantifier elimination

This paper adds to the discussion about theoretical aspects of particle swarm stability by proposing to employ stochastic Lyapunov functions and to determine the convergence set by quantifier elimination. We present a computational procedure and show that this approach leads to reevaluation and extension of previously know stability regions for PSO using a Lyapunov approach under stagnation assumptions.

Evolution of Cooperation for Multiple Mutant Configurations on All Regular Graphs with $N \leq 14$ players

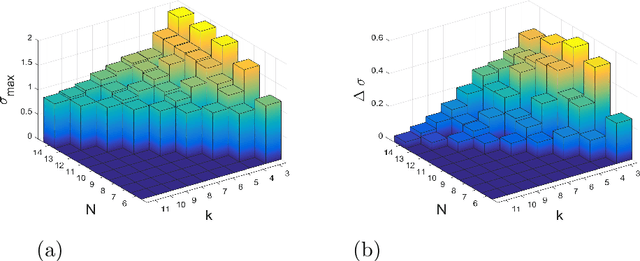
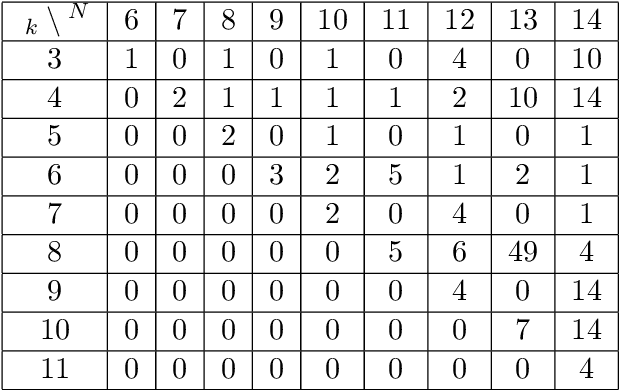
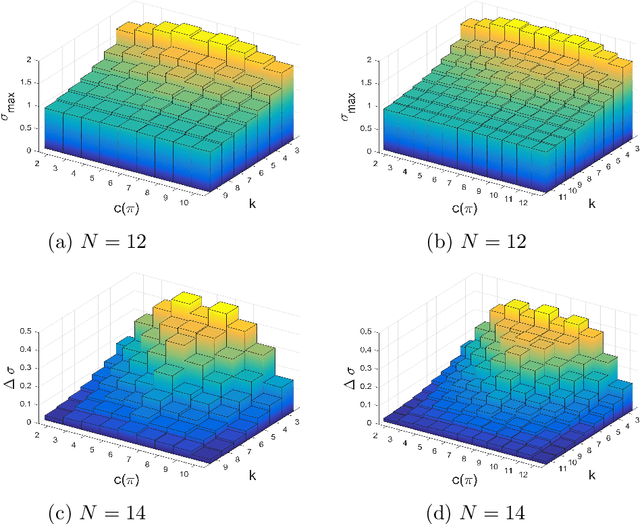
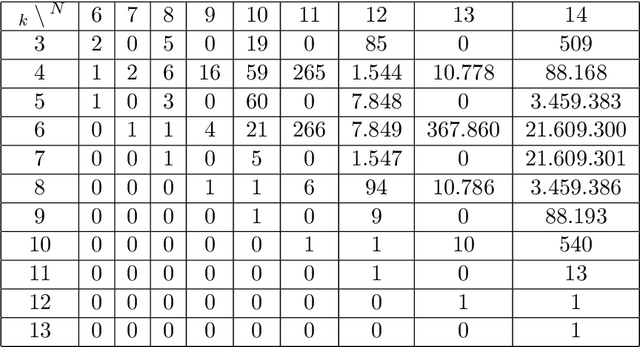
We study the emergence of cooperation in structured populations with any arrangement of cooperators and defectors on the evolutionary graph. Using structure coefficients defined for configurations describing such arrangements of any number of mutants, we provide results for weak selection to favor cooperation over defection on any regular graph with $N \leq 14$ vertices. Furthermore, the properties of graphs that particularly promote cooperation are analyzed. It is shown that the number of graph cycles of certain length is a good predictor for the values of the structure coefficient, and thus a tendency to favor cooperation. Another property of particularly cooperation-promoting regular graphs with a low degree is that they are structured to have blocks with clusters of mutants that are connected by cut vertices and/or hinge vertices.

Analyzing symmetry and symmetry breaking by computational aesthetic measures

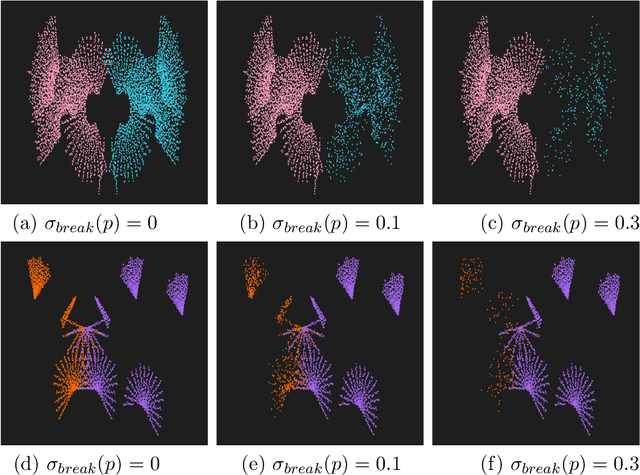
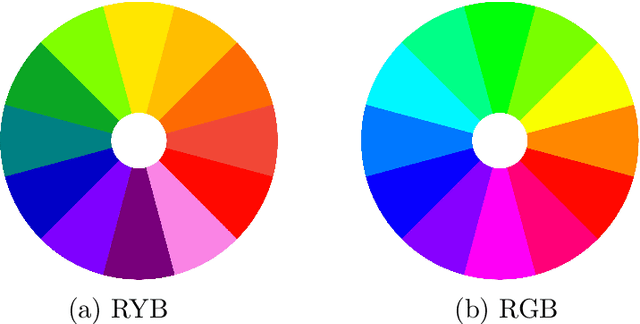
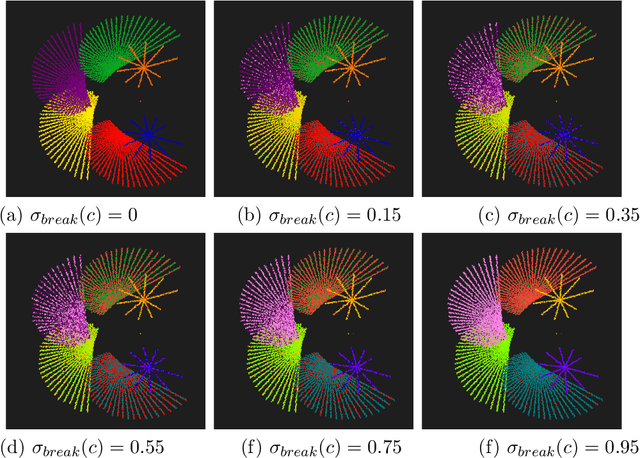
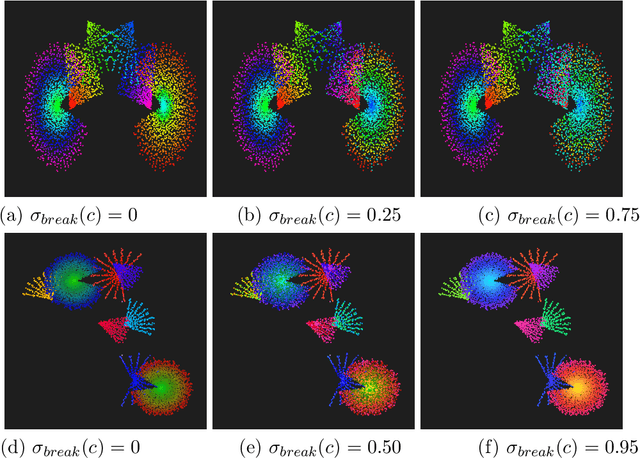
We study creating and analyzing symmetry and broken symmetry in digital art. Our focus is not so much on computer-generating artistic images, but rather on analyzing concepts and templates for incorporating symmetry and symmetry breaking into the creation process. Taking as a starting point patterns generated algorithmically by emulating the collective feeding behavior of sand-bubbler crabs, all four types of two-dimensional symmetry are used as isometric maps. Apart from a geometric interpretation of symmetry, we also consider color as an object of symmetric transformations. Color symmetry is realized as a color permutation consistent with the isometries. Moreover, we analyze the abilities of computational aesthetic measures to serve as a metric that reflects design parameters, i.e. the type of symmetry and the degree of symmetry breaking.

Relationships between dilemma strength and fixation properties in coevolutionary games

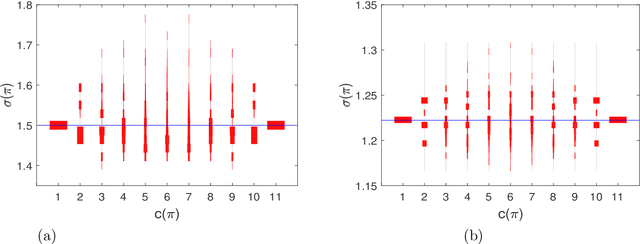
Whether or not cooperation is favored over defection in evolutionary games can be assigned by structure coefficients for any arrangement of cooperators and defectors on any network modeled as a regular graph. We study how these structure coefficients relate to a scaling of dilemma strength in social dilemma games. It is shown that some graphs permit certain arrangements of cooperators and defectors to possess particularly large structure coefficients. Moreover, these large coefficients imply particularly large sections of a bounded parameter plane spanned by scaling gamble-intending and risk-averting dilemma strength.

Fixation properties of multiple cooperator configurations on regular graphs

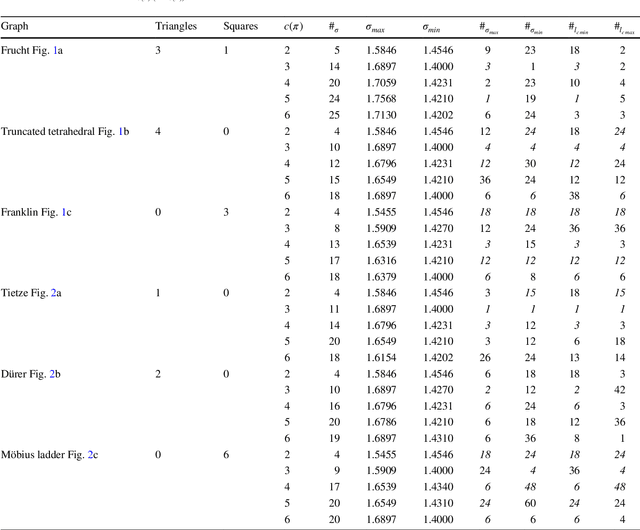
Whether or not cooperation is favored in evolutionary games on graphs depends on the population structure and spatial properties of the interaction network. Population structures can be expressed as configurations. Such configurations extend scenarios with a single cooperator among defectors to any number of cooperators and any arrangement of cooperators and defectors. Thus, as a single cooperator can be interpreted as a lone mutant, the discussion about fixation properties based on configurations also applies to multiple mutants. For interaction networks modeled as regular graphs and for weak selection, the emergence of cooperation can be assessed by structure coefficients, which are specific for a configuration and a graph. We analyze these structure coefficients and particularly show that under certain conditions the coefficients strongly correlate to the average shortest path length between cooperators on the evolutionary graph. Thus,for multiple cooperators fixation properties on regular evolutionary graphs can be linked to cooperator path length.