Fixation properties of multiple cooperator configurations on regular graphs
Paper and Code
Nov 16, 2018
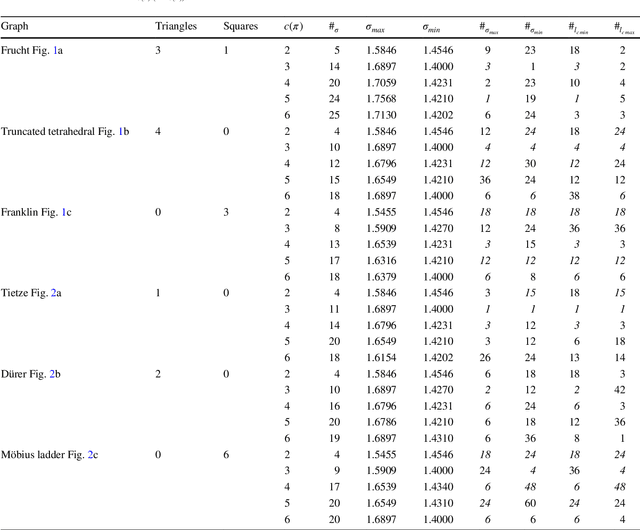
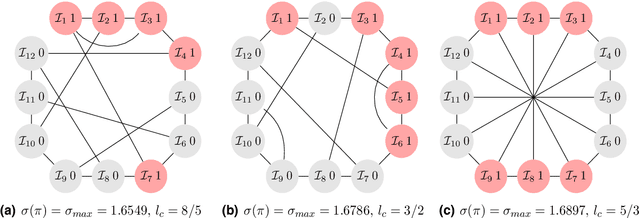

Whether or not cooperation is favored in evolutionary games on graphs depends on the population structure and spatial properties of the interaction network. Population structures can be expressed as configurations. Such configurations extend scenarios with a single cooperator among defectors to any number of cooperators and any arrangement of cooperators and defectors. Thus, as a single cooperator can be interpreted as a lone mutant, the discussion about fixation properties based on configurations also applies to multiple mutants. For interaction networks modeled as regular graphs and for weak selection, the emergence of cooperation can be assessed by structure coefficients, which are specific for a configuration and a graph. We analyze these structure coefficients and particularly show that under certain conditions the coefficients strongly correlate to the average shortest path length between cooperators on the evolutionary graph. Thus,for multiple cooperators fixation properties on regular evolutionary graphs can be linked to cooperator path length.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge