Analyzing symmetry and symmetry breaking by computational aesthetic measures
Paper and Code
Oct 15, 2019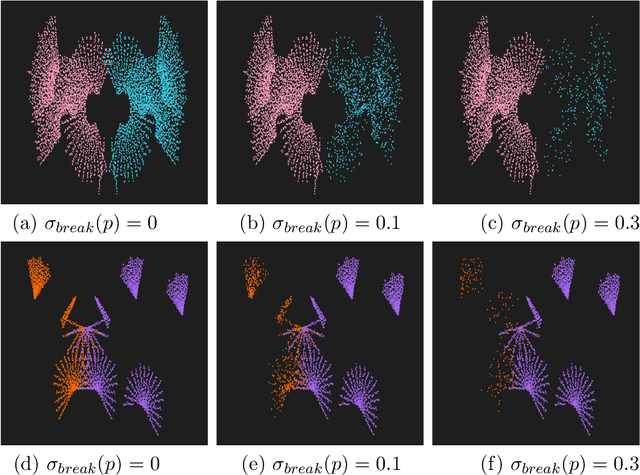
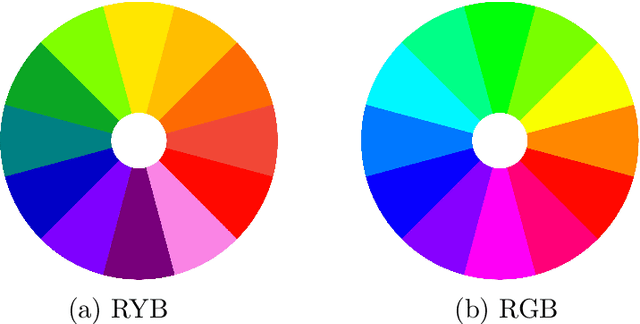
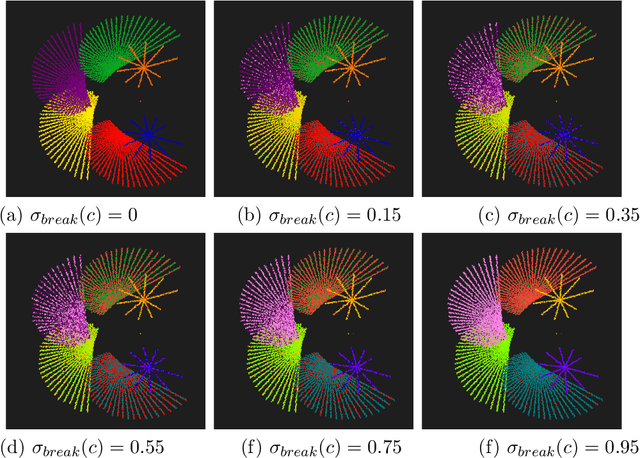
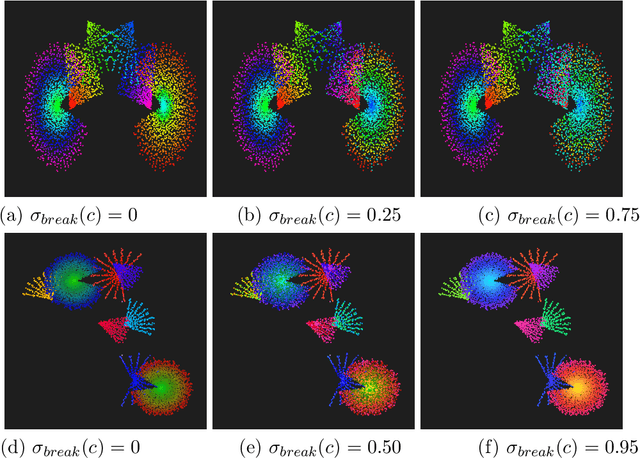
We study creating and analyzing symmetry and broken symmetry in digital art. Our focus is not so much on computer-generating artistic images, but rather on analyzing concepts and templates for incorporating symmetry and symmetry breaking into the creation process. Taking as a starting point patterns generated algorithmically by emulating the collective feeding behavior of sand-bubbler crabs, all four types of two-dimensional symmetry are used as isometric maps. Apart from a geometric interpretation of symmetry, we also consider color as an object of symmetric transformations. Color symmetry is realized as a color permutation consistent with the isometries. Moreover, we analyze the abilities of computational aesthetic measures to serve as a metric that reflects design parameters, i.e. the type of symmetry and the degree of symmetry breaking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge