Evolution of Cooperation for Multiple Mutant Configurations on All Regular Graphs with $N \leq 14$ players
Paper and Code
Nov 09, 2019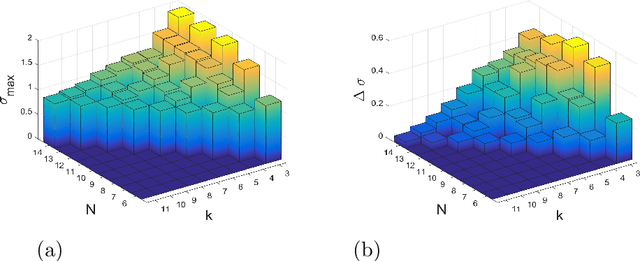
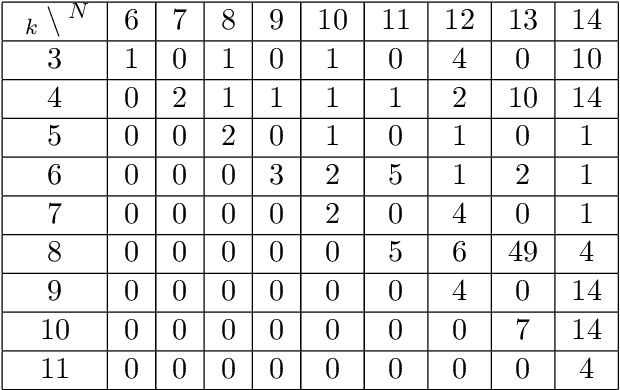
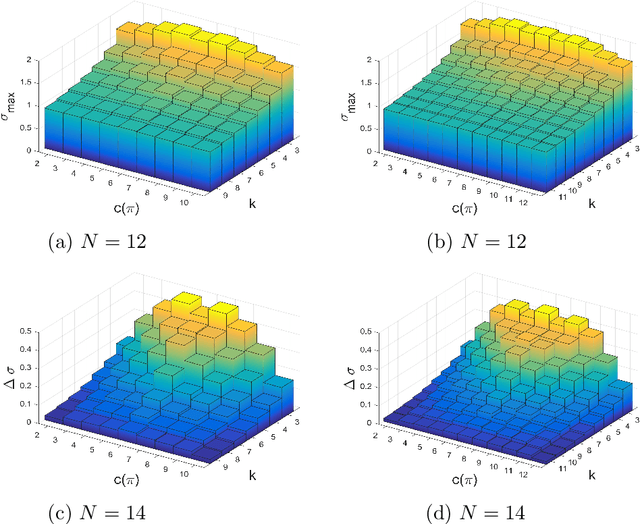
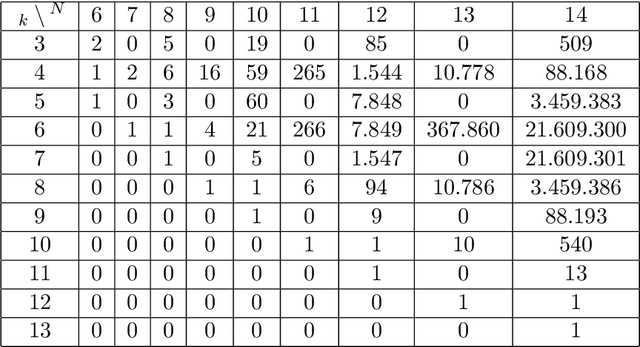
We study the emergence of cooperation in structured populations with any arrangement of cooperators and defectors on the evolutionary graph. Using structure coefficients defined for configurations describing such arrangements of any number of mutants, we provide results for weak selection to favor cooperation over defection on any regular graph with $N \leq 14$ vertices. Furthermore, the properties of graphs that particularly promote cooperation are analyzed. It is shown that the number of graph cycles of certain length is a good predictor for the values of the structure coefficient, and thus a tendency to favor cooperation. Another property of particularly cooperation-promoting regular graphs with a low degree is that they are structured to have blocks with clusters of mutants that are connected by cut vertices and/or hinge vertices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge