Multiresolution Neural Networks for Imaging

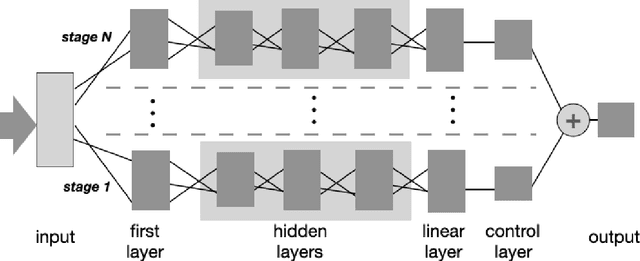
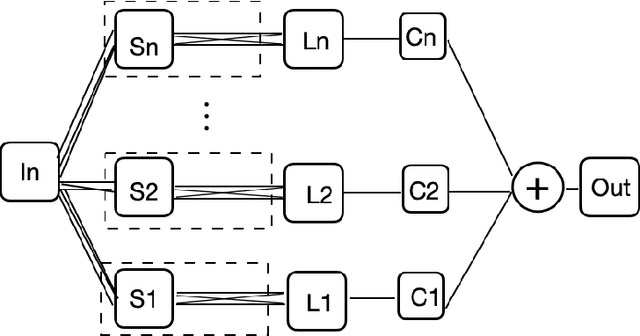
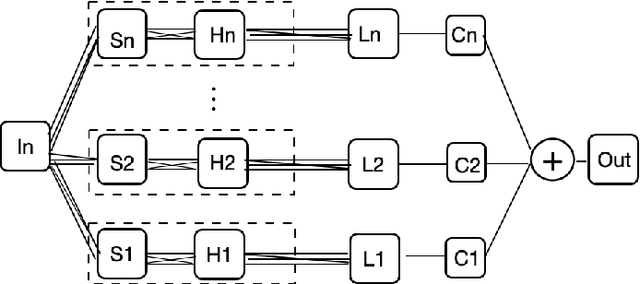
We present MR-Net, a general architecture for multiresolution neural networks, and a framework for imaging applications based on this architecture. Our coordinate-based networks are continuous both in space and in scale as they are composed of multiple stages that progressively add finer details. Besides that, they are a compact and efficient representation. We show examples of multiresolution image representation and applications to texturemagnification, minification, and antialiasing. This document is the extended version of the paper [PNS+22]. It includes additional material that would not fit the page limitations of the conference track for publication.

Towards Perspective-Based Specification of Machine Learning-Enabled Systems

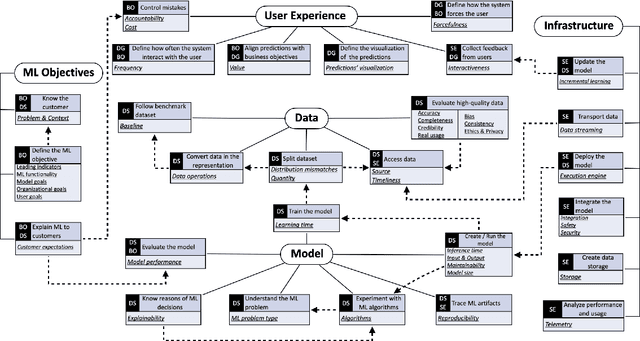
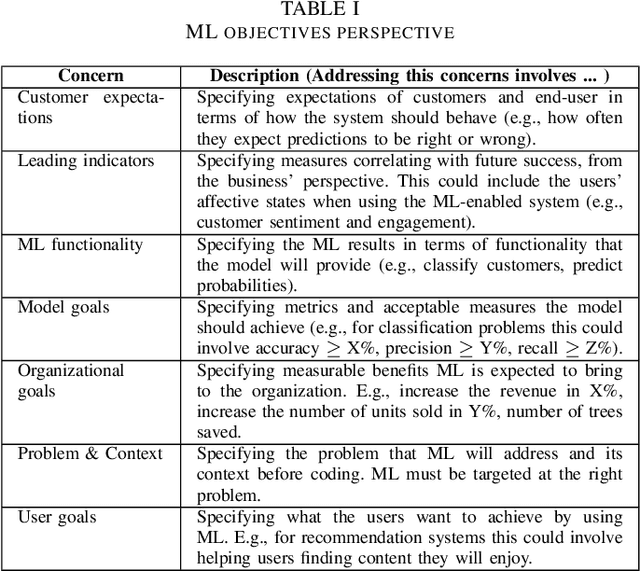
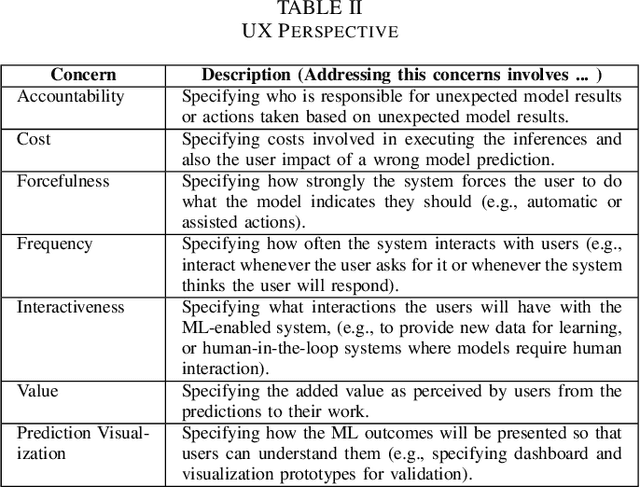
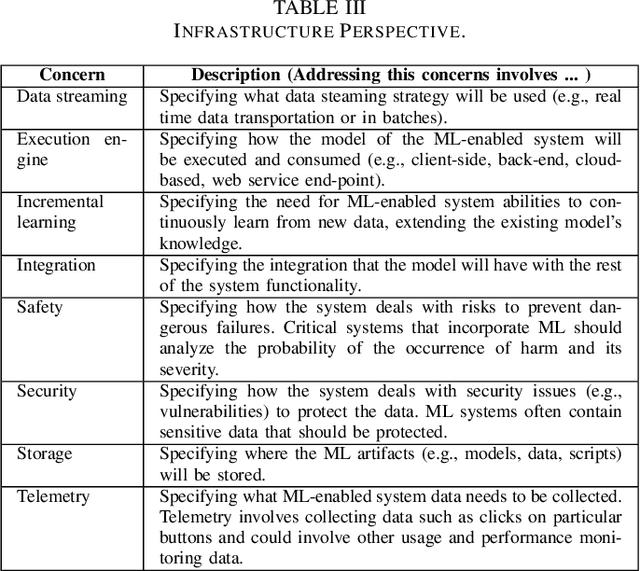
Machine learning (ML) teams often work on a project just to realize the performance of the model is not good enough. Indeed, the success of ML-enabled systems involves aligning data with business problems, translating them into ML tasks, experimenting with algorithms, evaluating models, capturing data from users, among others. Literature has shown that ML-enabled systems are rarely built based on precise specifications for such concerns, leading ML teams to become misaligned due to incorrect assumptions, which may affect the quality of such systems and overall project success. In order to help addressing this issue, this paper describes our work towards a perspective-based approach for specifying ML-enabled systems. The approach involves analyzing a set of 45 ML concerns grouped into five perspectives: objectives, user experience, infrastructure, model, and data. The main contribution of this paper is to provide two new artifacts that can be used to help specifying ML-enabled systems: (i) the perspective-based ML task and concern diagram and (ii) the perspective-based ML specification template.

Neural Implicit Surfaces in Higher Dimension

This work investigates the use of neural networks admitting high-order derivatives for modeling dynamic variations of smooth implicit surfaces. For this purpose, it extends the representation of differentiable neural implicit surfaces to higher dimensions, which opens up mechanisms that allow to exploit geometric transformations in many settings, from animation and surface evolution to shape morphing and design galleries. The problem is modeled by a $k$-parameter family of surfaces $S_c$, specified as a neural network function $f : \mathbb{R}^3 \times \mathbb{R}^k \rightarrow \mathbb{R}$, where $S_c$ is the zero-level set of the implicit function $f(\cdot, c) : \mathbb{R}^3 \rightarrow \mathbb{R} $, with $c \in \mathbb{R}^k$, with variations induced by the control variable $c$. In that context, restricted to each coordinate of $\mathbb{R}^k$, the underlying representation is a neural homotopy which is the solution of a general partial differential equation.

Differential Geometry in Neural Implicits

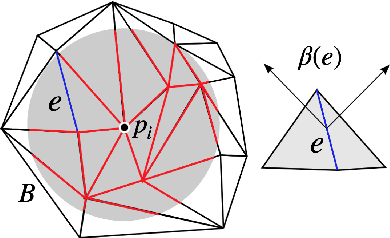
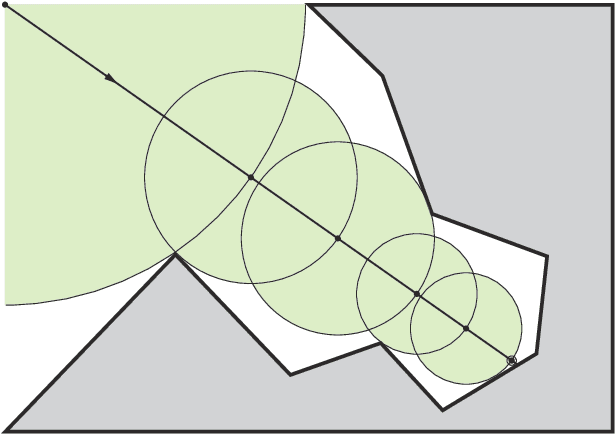
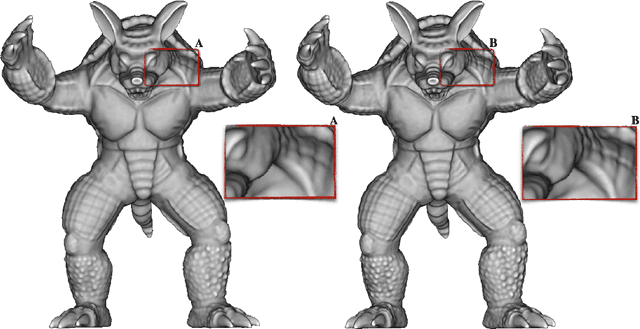
We introduce a neural implicit framework that bridges discrete differential geometry of triangle meshes and continuous differential geometry of neural implicit surfaces. It exploits the differentiable properties of neural networks and the discrete geometry of triangle meshes to approximate them as the zero-level sets of neural implicit functions. To train a neural implicit function, we propose a loss function that allows terms with high-order derivatives, such as the alignment between the principal directions, to learn more geometric details. During training, we consider a non-uniform sampling strategy based on the discrete curvatures of the triangle mesh to access points with more geometric details. This sampling implies faster learning while preserving geometric accuracy. We present the analytical differential geometry formulas for neural surfaces, such as normal vectors and curvatures. We use them to render the surfaces using sphere tracing. Additionally, we propose a network optimization based on singular value decomposition to reduce the number of parameters.