Neural Implicit Surfaces in Higher Dimension

This work investigates the use of neural networks admitting high-order derivatives for modeling dynamic variations of smooth implicit surfaces. For this purpose, it extends the representation of differentiable neural implicit surfaces to higher dimensions, which opens up mechanisms that allow to exploit geometric transformations in many settings, from animation and surface evolution to shape morphing and design galleries. The problem is modeled by a $k$-parameter family of surfaces $S_c$, specified as a neural network function $f : \mathbb{R}^3 \times \mathbb{R}^k \rightarrow \mathbb{R}$, where $S_c$ is the zero-level set of the implicit function $f(\cdot, c) : \mathbb{R}^3 \rightarrow \mathbb{R} $, with $c \in \mathbb{R}^k$, with variations induced by the control variable $c$. In that context, restricted to each coordinate of $\mathbb{R}^k$, the underlying representation is a neural homotopy which is the solution of a general partial differential equation.

Differential Geometry in Neural Implicits

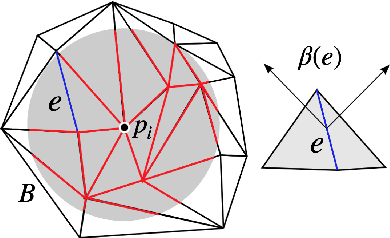
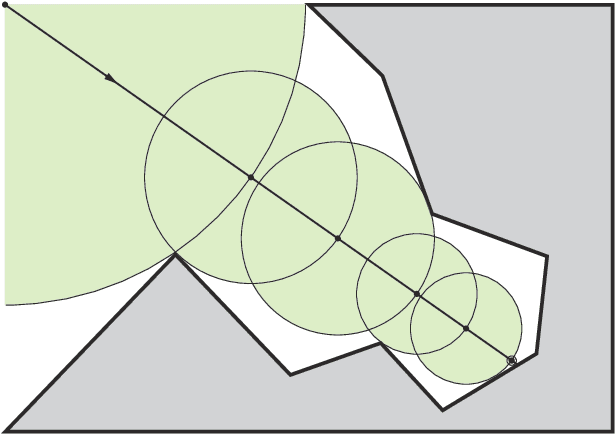
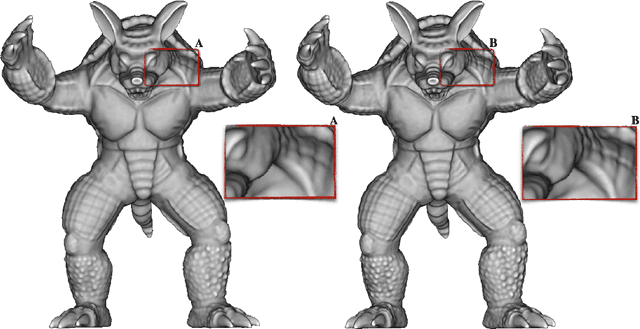
We introduce a neural implicit framework that bridges discrete differential geometry of triangle meshes and continuous differential geometry of neural implicit surfaces. It exploits the differentiable properties of neural networks and the discrete geometry of triangle meshes to approximate them as the zero-level sets of neural implicit functions. To train a neural implicit function, we propose a loss function that allows terms with high-order derivatives, such as the alignment between the principal directions, to learn more geometric details. During training, we consider a non-uniform sampling strategy based on the discrete curvatures of the triangle mesh to access points with more geometric details. This sampling implies faster learning while preserving geometric accuracy. We present the analytical differential geometry formulas for neural surfaces, such as normal vectors and curvatures. We use them to render the surfaces using sphere tracing. Additionally, we propose a network optimization based on singular value decomposition to reduce the number of parameters.