Heather G. Patsolic
Seeded Graph Matching
Apr 10, 2018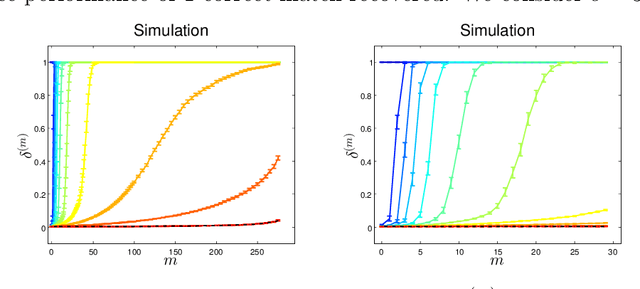
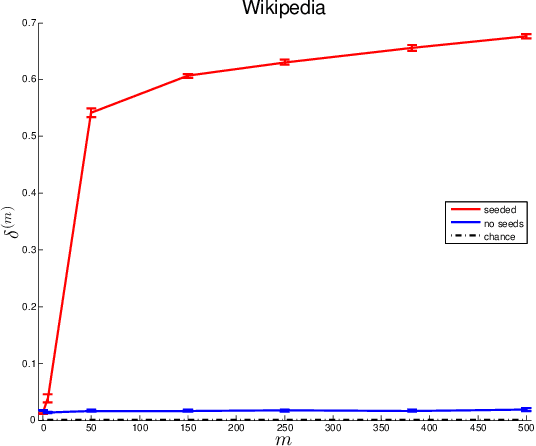

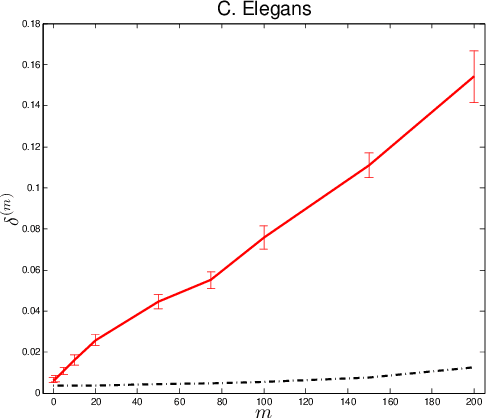
Abstract:Given two graphs, the graph matching problem is to align the two vertex sets so as to minimize the number of adjacency disagreements between the two graphs. The seeded graph matching problem is the graph matching problem when we are first given a partial alignment that we are tasked with completing. In this paper, we modify the state-of-the-art approximate graph matching algorithm "FAQ" of Vogelstein et al. (2015) to make it a fast approximate seeded graph matching algorithm, adapt its applicability to include graphs with differently sized vertex sets, and extend the algorithm so as to provide, for each individual vertex, a nomination list of likely matches. We demonstrate the effectiveness of our algorithm via simulation and real data experiments; indeed, knowledge of even a few seeds can be extremely effective when our seeded graph matching algorithm is used to recover a naturally existing alignment that is only partially observed.
Vertex Nomination Via Local Neighborhood Matching
Jul 22, 2017



Abstract:Consider two networks on overlapping, non-identical vertex sets. Given vertices of interest in the first network, we seek to identify the corresponding vertices, if any exist, in the second network. While in moderately sized networks graph matching methods can be applied directly to recover the missing correspondences, herein we present a principled methodology appropriate for situations in which the networks are too large for brute-force graph matching. Our methodology identifies vertices in a local neighborhood of the vertices of interest in the first network that have verifiable corresponding vertices in the second network. Leveraging these known correspondences, referred to as seeds, we match the induced subgraphs in each network generated by the neighborhoods of these verified seeds, and rank the vertices of the second network in terms of the most likely matches to the original vertices of interest. We demonstrate the applicability of our methodology through simulations and real data examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge