Multi-View Majority Vote Learning Algorithms: Direct Minimization of PAC-Bayesian Bounds

The PAC-Bayesian framework has significantly advanced our understanding of statistical learning, particularly in majority voting methods. However, its application to multi-view learning remains underexplored. In this paper, we extend PAC-Bayesian theory to the multi-view setting, introducing novel PAC-Bayesian bounds based on R\'enyi divergence. These bounds improve upon traditional Kullback-Leibler divergence and offer more refined complexity measures. We further propose first and second-order oracle PAC-Bayesian bounds, along with an extension of the C-bound for multi-view learning. To ensure practical applicability, we develop efficient optimization algorithms with self-bounding properties.

PAC-Bayesian Domain Adaptation Bounds for Multi-view learning

This paper presents a series of new results for domain adaptation in the multi-view learning setting. The incorporation of multiple views in the domain adaptation was paid little attention in the previous studies. In this way, we propose an analysis of generalization bounds with Pac-Bayesian theory to consolidate the two paradigms, which are currently treated separately. Firstly, building on previous work by Germain et al., we adapt the distance between distribution proposed by Germain et al. for domain adaptation with the concept of multi-view learning. Thus, we introduce a novel distance that is tailored for the multi-view domain adaptation setting. Then, we give Pac-Bayesian bounds for estimating the introduced divergence. Finally, we compare the different new bounds with the previous studies.

An Experimental Comparison of Hybrid Algorithms for Bayesian Network Structure Learning

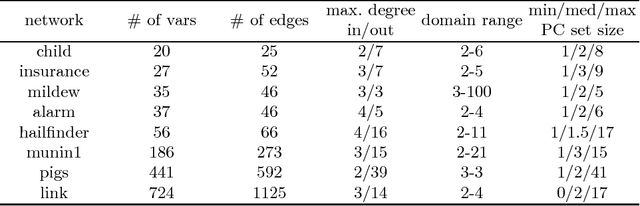
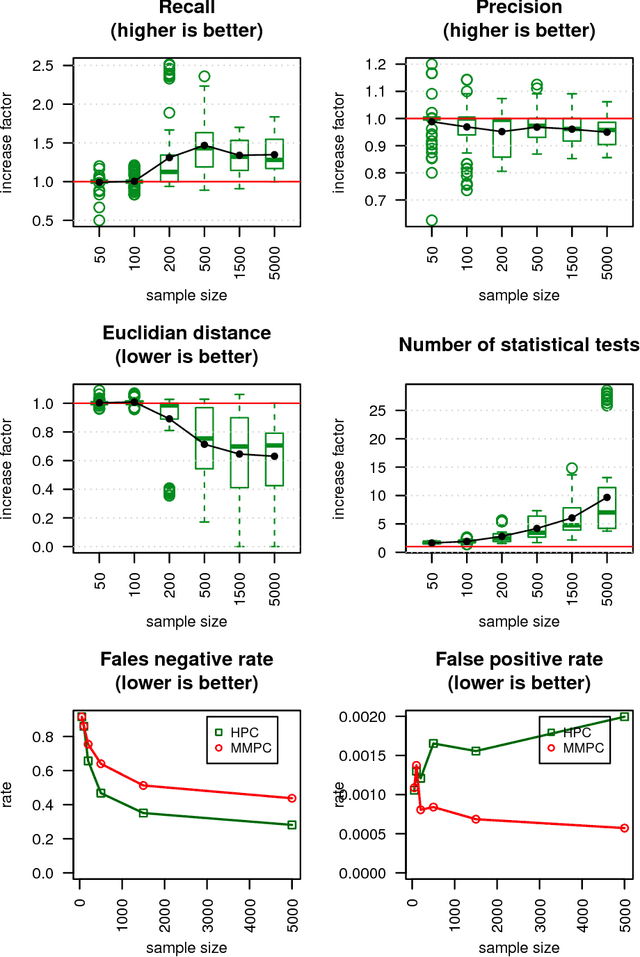
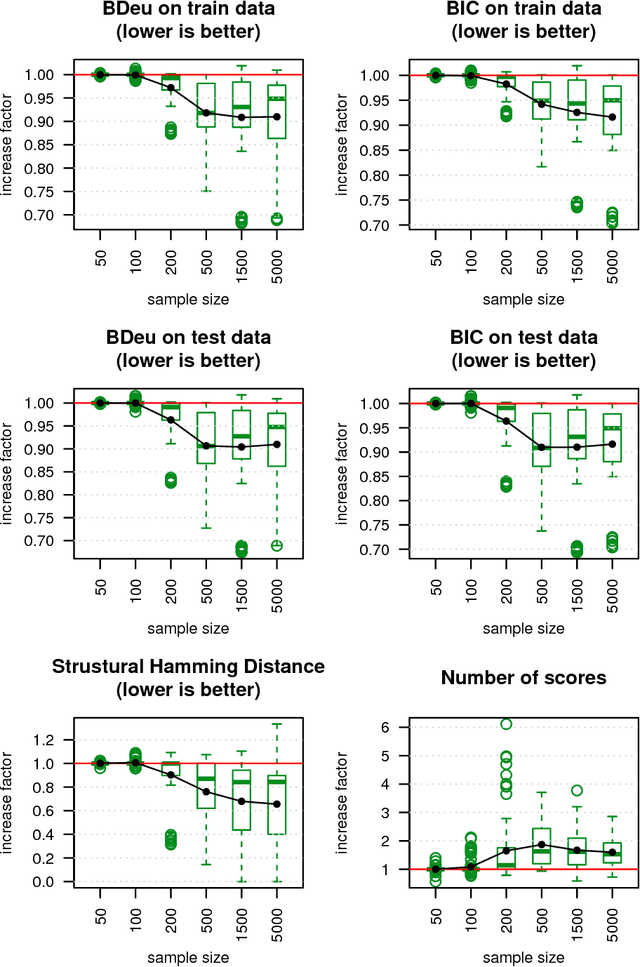
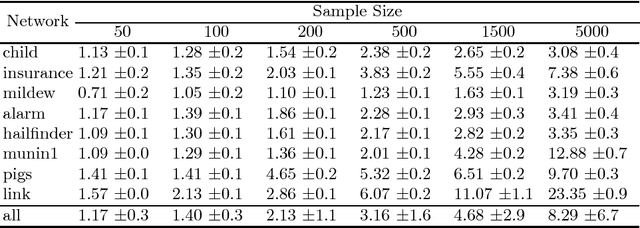
We present a novel hybrid algorithm for Bayesian network structure learning, called Hybrid HPC (H2PC). It first reconstructs the skeleton of a Bayesian network and then performs a Bayesian-scoring greedy hill-climbing search to orient the edges. It is based on a subroutine called HPC, that combines ideas from incremental and divide-and-conquer constraint-based methods to learn the parents and children of a target variable. We conduct an experimental comparison of H2PC against Max-Min Hill-Climbing (MMHC), which is currently the most powerful state-of-the-art algorithm for Bayesian network structure learning, on several benchmarks with various data sizes. Our extensive experiments show that H2PC outperforms MMHC both in terms of goodness of fit to new data and in terms of the quality of the network structure itself, which is closer to the true dependence structure of the data. The source code (in R) of H2PC as well as all data sets used for the empirical tests are publicly available.

A hybrid algorithm for Bayesian network structure learning with application to multi-label learning

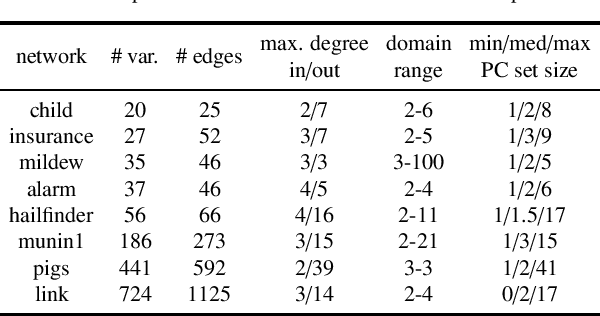
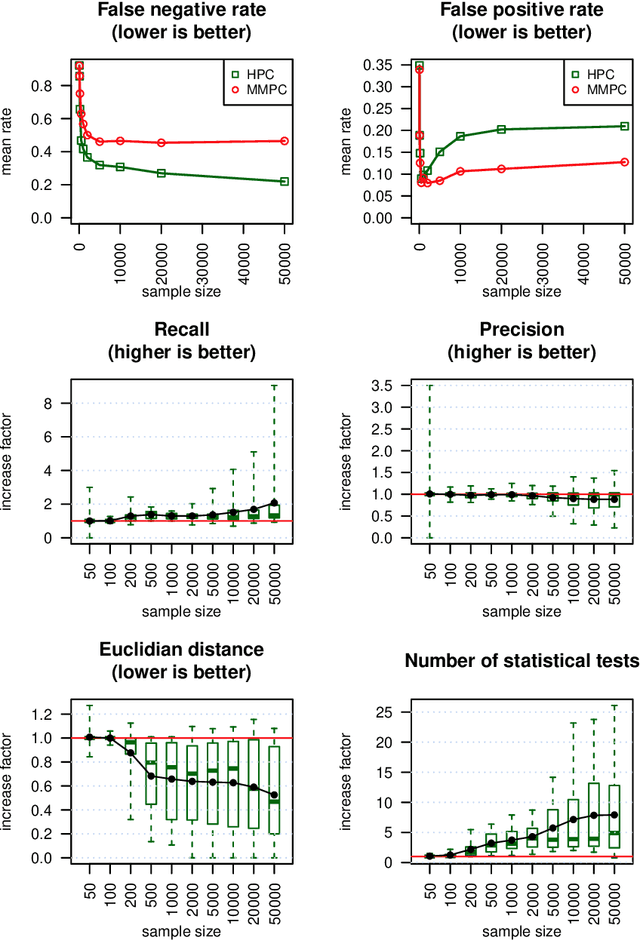
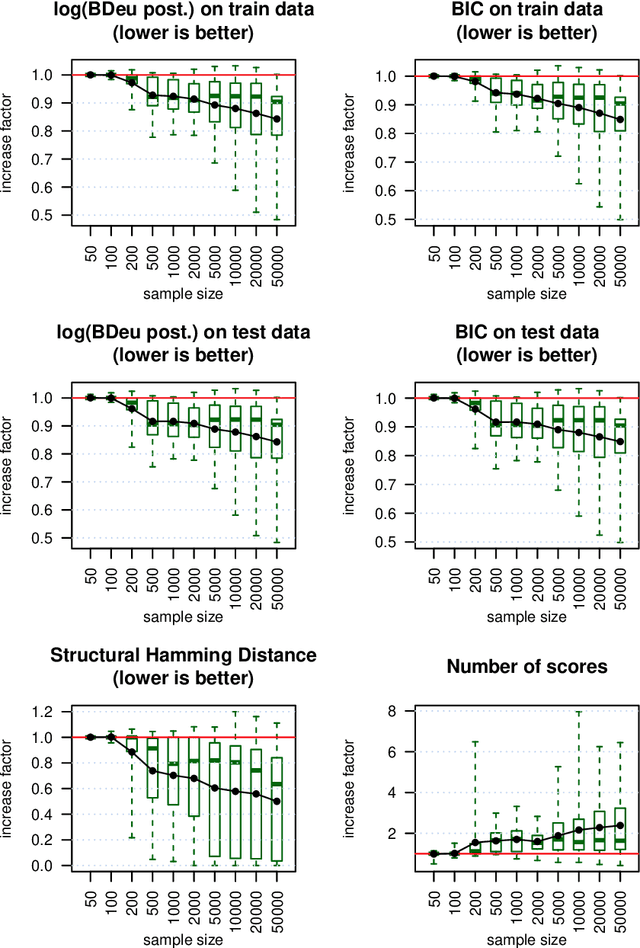
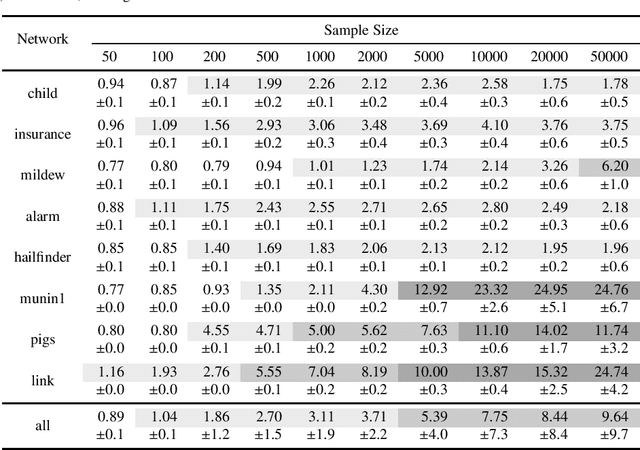
We present a novel hybrid algorithm for Bayesian network structure learning, called H2PC. It first reconstructs the skeleton of a Bayesian network and then performs a Bayesian-scoring greedy hill-climbing search to orient the edges. The algorithm is based on divide-and-conquer constraint-based subroutines to learn the local structure around a target variable. We conduct two series of experimental comparisons of H2PC against Max-Min Hill-Climbing (MMHC), which is currently the most powerful state-of-the-art algorithm for Bayesian network structure learning. First, we use eight well-known Bayesian network benchmarks with various data sizes to assess the quality of the learned structure returned by the algorithms. Our extensive experiments show that H2PC outperforms MMHC in terms of goodness of fit to new data and quality of the network structure with respect to the true dependence structure of the data. Second, we investigate H2PC's ability to solve the multi-label learning problem. We provide theoretical results to characterize and identify graphically the so-called minimal label powersets that appear as irreducible factors in the joint distribution under the faithfulness condition. The multi-label learning problem is then decomposed into a series of multi-class classification problems, where each multi-class variable encodes a label powerset. H2PC is shown to compare favorably to MMHC in terms of global classification accuracy over ten multi-label data sets covering different application domains. Overall, our experiments support the conclusions that local structural learning with H2PC in the form of local neighborhood induction is a theoretically well-motivated and empirically effective learning framework that is well suited to multi-label learning. The source code (in R) of H2PC as well as all data sets used for the empirical tests are publicly available.