An Experimental Comparison of Hybrid Algorithms for Bayesian Network Structure Learning
Paper and Code
Aug 24, 2015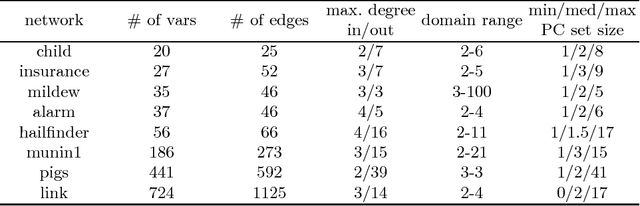
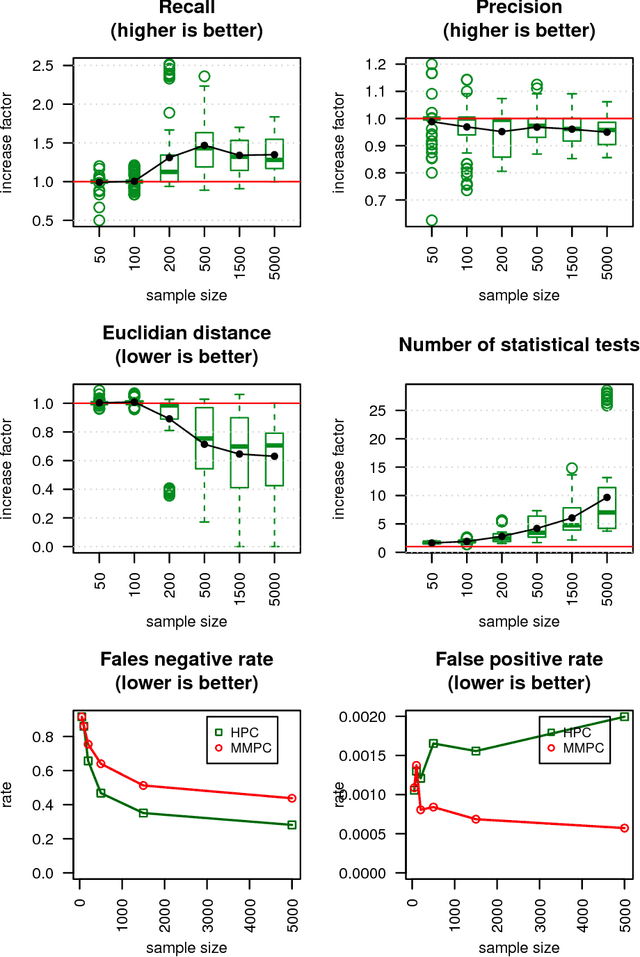
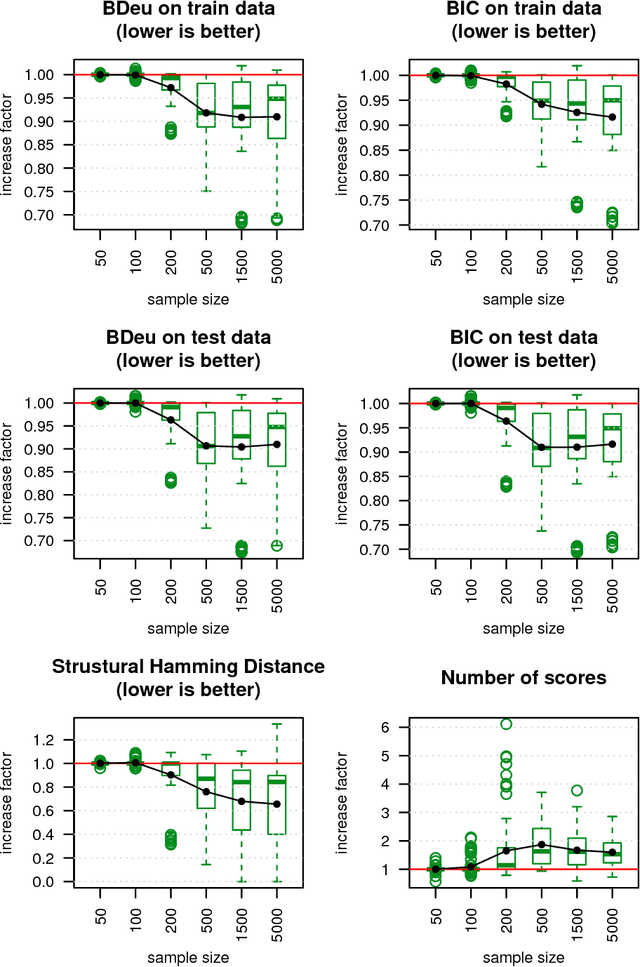
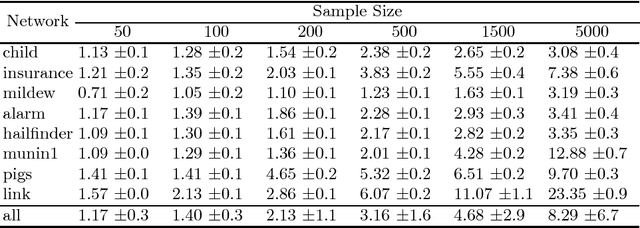
We present a novel hybrid algorithm for Bayesian network structure learning, called Hybrid HPC (H2PC). It first reconstructs the skeleton of a Bayesian network and then performs a Bayesian-scoring greedy hill-climbing search to orient the edges. It is based on a subroutine called HPC, that combines ideas from incremental and divide-and-conquer constraint-based methods to learn the parents and children of a target variable. We conduct an experimental comparison of H2PC against Max-Min Hill-Climbing (MMHC), which is currently the most powerful state-of-the-art algorithm for Bayesian network structure learning, on several benchmarks with various data sizes. Our extensive experiments show that H2PC outperforms MMHC both in terms of goodness of fit to new data and in terms of the quality of the network structure itself, which is closer to the true dependence structure of the data. The source code (in R) of H2PC as well as all data sets used for the empirical tests are publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge