Mix and Match: A Novel FPGA-Centric Deep Neural Network Quantization Framework

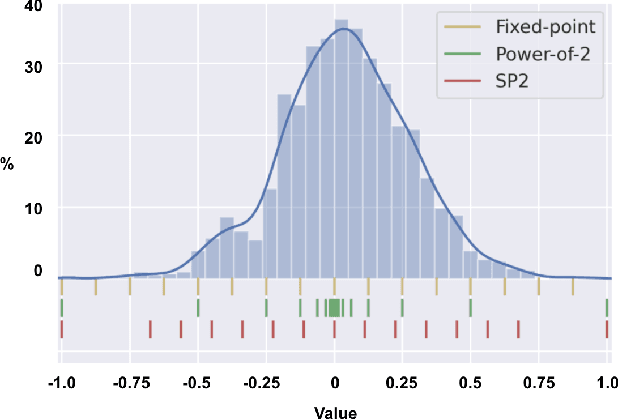
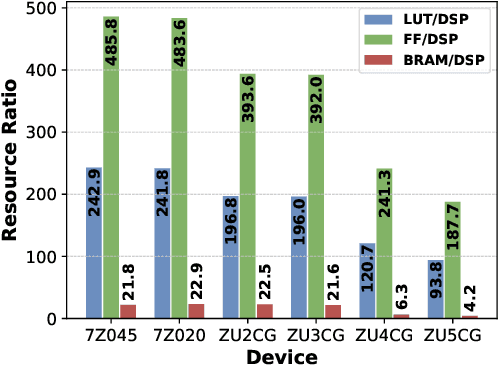
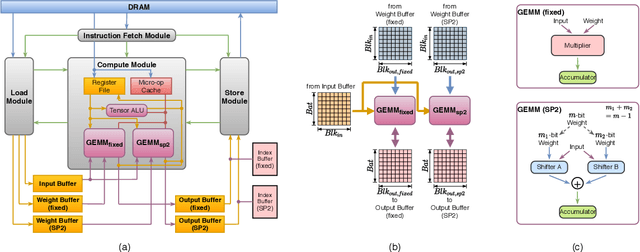
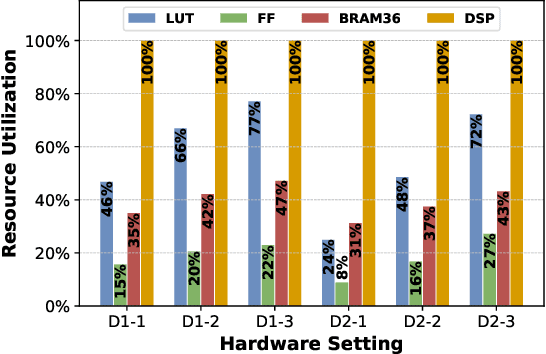
Deep Neural Networks (DNNs) have achieved extraordinary performance in various application domains. To support diverse DNN models, efficient implementations of DNN inference on edge-computing platforms, e.g., ASICs, FPGAs, and embedded systems, are extensively investigated. Due to the huge model size and computation amount, model compression is a critical step to deploy DNN models on edge devices. This paper focuses on weight quantization, a hardware-friendly model compression approach that is complementary to weight pruning. Unlike existing methods that use the same quantization scheme for all weights, we propose the first solution that applies different quantization schemes for different rows of the weight matrix. It is motivated by (1) the distribution of the weights in the different rows are not the same; and (2) the potential of achieving better utilization of heterogeneous FPGA hardware resources. To achieve that, we first propose a hardware-friendly quantization scheme named sum-of-power-of-2 (SP2) suitable for Gaussian-like weight distribution, in which the multiplication arithmetic can be replaced with logic shifter and adder, thereby enabling highly efficient implementations with the FPGA LUT resources. In contrast, the existing fixed-point quantization is suitable for Uniform-like weight distribution and can be implemented efficiently by DSP. Then to fully explore the resources, we propose an FPGA-centric mixed scheme quantization (MSQ) with an ensemble of the proposed SP2 and the fixed-point schemes. Combining the two schemes can maintain, or even increase accuracy due to better matching with weight distributions.

High-dimensional Dense Residual Convolutional Neural Network for Light Field Reconstruction

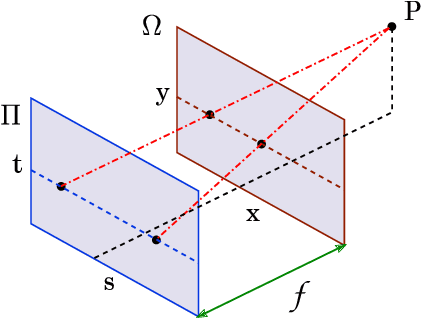
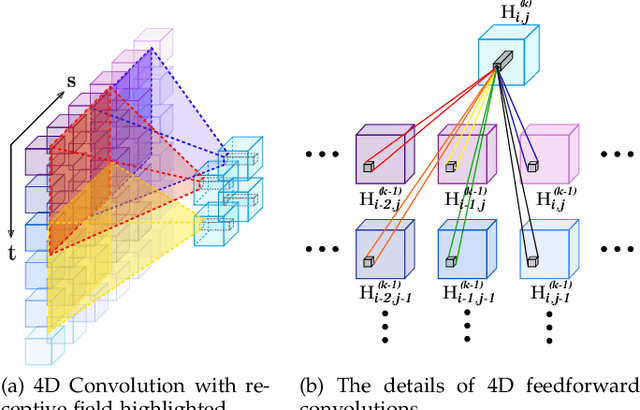
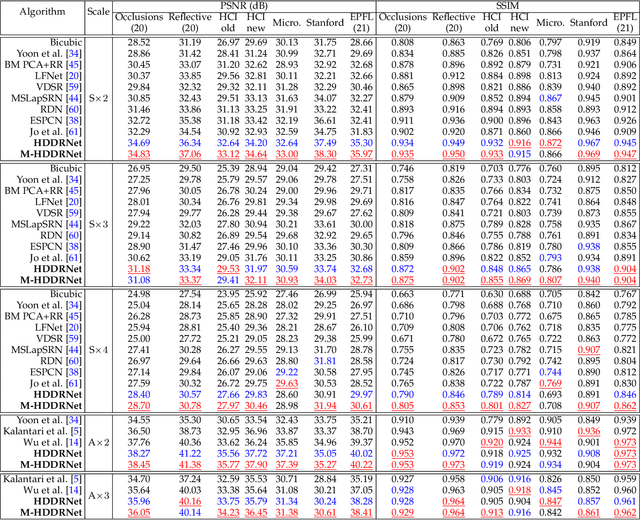
We consider the problem of high-dimensional light field reconstruction and develop a learning-based framework for spatial and angular super-resolution. Many current approaches either require disparity clues or restore the spatial and angular details separately. Such methods have difficulties with non-Lambertian surfaces or occlusions. In contrast, we formulate light field super-resolution (LFSR) as tensor restoration and develop a learning framework based on a two-stage restoration with 4-dimensional (4D) convolution. This allows our model to learn the features capturing the geometry information encoded in multiple adjacent views. Such geometric features vary near the occlusion regions and indicate the foreground object border. To train a feasible network, we propose a novel normalization operation based on a group of views in the feature maps, design a stage-wise loss function, and develop the multi-range training strategy to further improve the performance. Evaluations are conducted on a number of light field datasets including real-world scenes, synthetic data, and microscope light fields. The proposed method achieves superior performance and less execution time comparing with other state-of-the-art schemes.

Consistency Analysis for the Doubly Stochastic Dirichlet Process

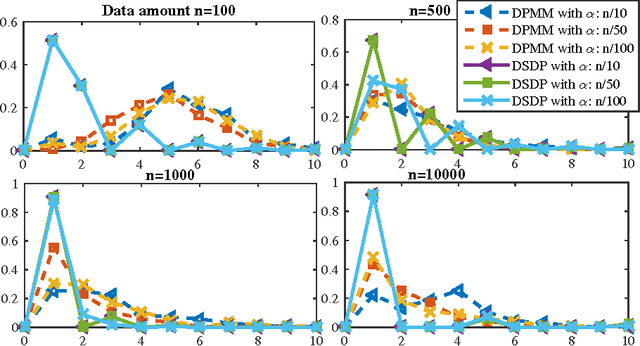
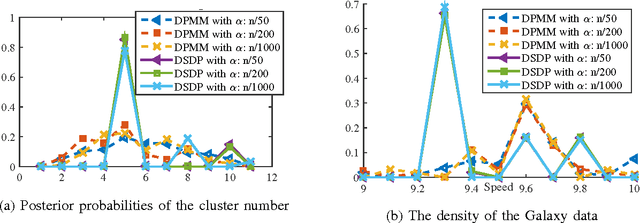
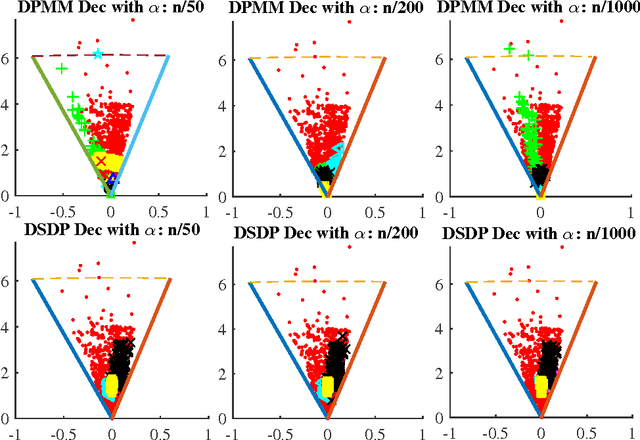
This technical report proves components consistency for the Doubly Stochastic Dirichlet Process with exponential convergence of posterior probability. We also present the fundamental properties for DSDP as well as inference algorithms. Simulation toy experiment and real-world experiment results for single and multi-cluster also support the consistency proof. This report is also a support document for the paper "Computationally Efficient Hyperspectral Data Learning Based on the Doubly Stochastic Dirichlet Process".