Fast Hyperspectral Neutron Tomography

Hyperspectral neutron computed tomography is a tomographic imaging technique in which thousands of wavelength-specific neutron radiographs are typically measured for each tomographic view. In conventional hyperspectral reconstruction, data from each neutron wavelength bin is reconstructed separately, which is extremely time-consuming. These reconstructions often suffer from poor quality due to low signal-to-noise ratio. Consequently, material decomposition based on these reconstructions tends to lead to both inaccurate estimates of the material spectra and inaccurate volumetric material separation. In this paper, we present two novel algorithms for processing hyperspectral neutron data: fast hyperspectral reconstruction and fast material decomposition. Both algorithms rely on a subspace decomposition procedure that transforms hyperspectral views into low-dimensional projection views within an intermediate subspace, where tomographic reconstruction is performed. The use of subspace decomposition dramatically reduces reconstruction time while reducing both noise and reconstruction artifacts. We apply our algorithms to both simulated and measured neutron data and demonstrate that they reduce computation and improve the quality of the results relative to conventional methods.

Autonomous Polycrystalline Material Decomposition for Hyperspectral Neutron Tomography

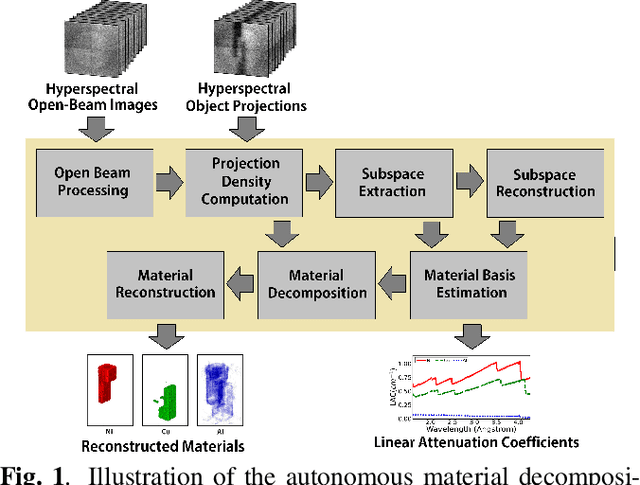
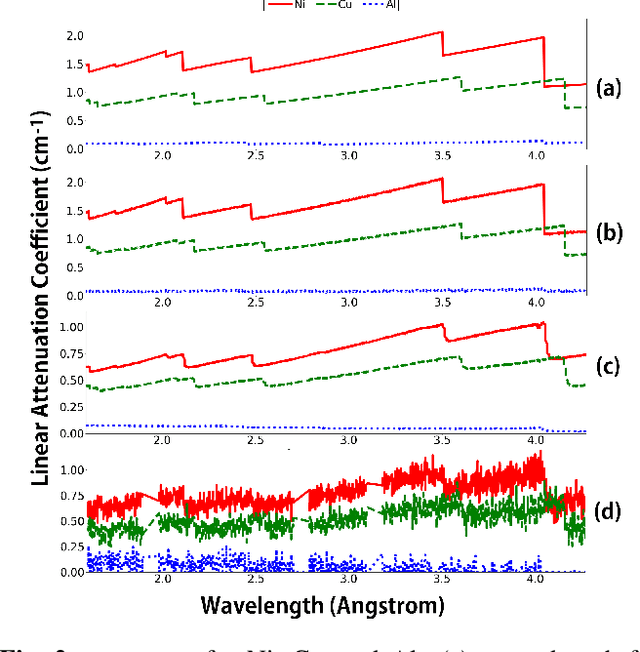
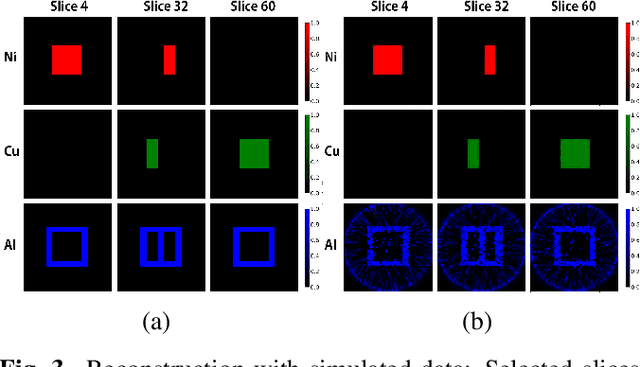
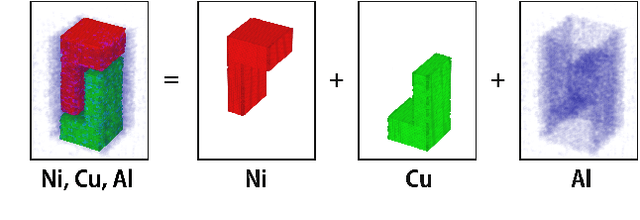
Hyperspectral neutron tomography is an effective method for analyzing crystalline material samples with complex compositions in a non-destructive manner. Since the counts in the hyperspectral neutron radiographs directly depend on the neutron cross-sections, materials may exhibit contrasting neutron responses across wavelengths. Therefore, it is possible to extract the unique signatures associated with each material and use them to separate the crystalline phases simultaneously. We introduce an autonomous material decomposition (AMD) algorithm to automatically characterize and localize polycrystalline structures using Bragg edges with contrasting neutron responses from hyperspectral data. The algorithm estimates the linear attenuation coefficient spectra from the measured radiographs and then uses these spectra to perform polycrystalline material decomposition and reconstructs 3D material volumes to localize materials in the spatial domain. Our results demonstrate that the method can accurately estimate both the linear attenuation coefficient spectra and associated reconstructions on both simulated and experimental neutron data.

An Edge Alignment-based Orientation Selection Method for Neutron Tomography

Neutron computed tomography (nCT) is a 3D characterization technique used to image the internal morphology or chemical composition of samples in biology and materials sciences. A typical workflow involves placing the sample in the path of a neutron beam, acquiring projection data at a predefined set of orientations, and processing the resulting data using an analytic reconstruction algorithm. Typical nCT scans require hours to days to complete and are then processed using conventional filtered back-projection (FBP), which performs poorly with sparse views or noisy data. Hence, the main methods in order to reduce overall acquisition time are the use of an improved sampling strategy combined with the use of advanced reconstruction methods such as model-based iterative reconstruction (MBIR). In this paper, we propose an adaptive orientation selection method in which an MBIR reconstruction on previously-acquired measurements is used to define an objective function on orientations that balances a data-fitting term promoting edge alignment and a regularization term promoting orientation diversity. Using simulated and experimental data, we demonstrate that our method produces high-quality reconstructions using significantly fewer total measurements than the conventional approach.