Gradient scarcity with Bilevel Optimization for Graph Learning

A common issue in graph learning under the semi-supervised setting is referred to as gradient scarcity. That is, learning graphs by minimizing a loss on a subset of nodes causes edges between unlabelled nodes that are far from labelled ones to receive zero gradients. The phenomenon was first described when optimizing the graph and the weights of a Graph Neural Network (GCN) with a joint optimization algorithm. In this work, we give a precise mathematical characterization of this phenomenon, and prove that it also emerges in bilevel optimization, where additional dependency exists between the parameters of the problem. While for GCNs gradient scarcity occurs due to their finite receptive field, we show that it also occurs with the Laplacian regularization model, in the sense that gradients amplitude decreases exponentially with distance to labelled nodes. To alleviate this issue, we study several solutions: we propose to resort to latent graph learning using a Graph-to-Graph model (G2G), graph regularization to impose a prior structure on the graph, or optimizing on a larger graph than the original one with a reduced diameter. Our experiments on synthetic and real datasets validate our analysis and prove the efficiency of the proposed solutions.

Supervised learning of analysis-sparsity priors with automatic differentiation

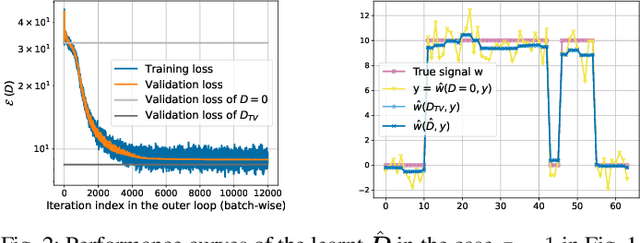
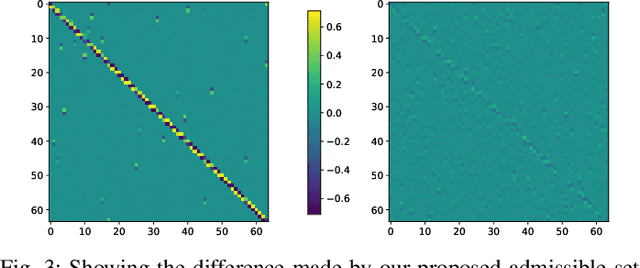
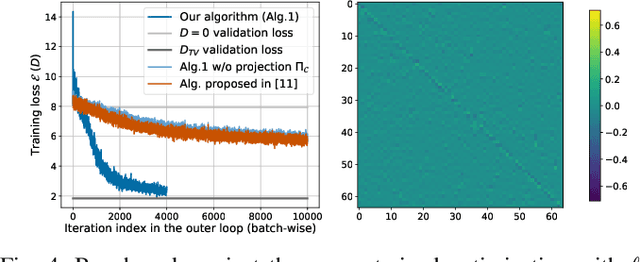
Sparsity priors are commonly used in denoising and image reconstruction. For analysis-type priors, a dictionary defines a representation of signals that is likely to be sparse. In most situations, this dictionary is not known, and is to be recovered from pairs of ground-truth signals and measurements, by minimizing the reconstruction error. This defines a hierarchical optimization problem, which can be cast as a bi-level optimization. Yet, this problem is unsolvable, as reconstructions and their derivative wrt the dictionary have no closed-form expression. However, reconstructions can be iteratively computed using the Forward-Backward splitting (FB) algorithm. In this paper, we approximate reconstructions by the output of the aforementioned FB algorithm. Then, we leverage automatic differentiation to evaluate the gradient of this output wrt the dictionary, which we learn with projected gradient descent. Experiments show that our algorithm successfully learns the 1D Total Variation (TV) dictionary from piecewise constant signals. For the same case study, we propose to constrain our search to dictionaries of 0-centered columns, which removes undesired local minima and improves numerical stability.

Fast Graph Kernel with Optical Random Features

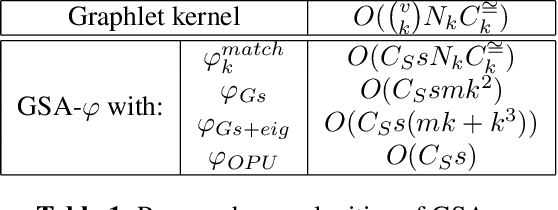
The graphlet kernel is a classical method in graph classification. It however suffers from a high computation cost due to the isomorphism test it includes. As a generic proxy, and in general at the cost of losing some information, this test can be efficiently replaced by a user-defined mapping that computes various graph characteristics. In this paper, we propose to leverage kernel random features within the graphlet framework, and establish a theoretical link with a mean kernel metric. If this method can still be prohibitively costly for usual random features, we then incorporate optical random features that can be computed in constant time. Experiments show that the resulting algorithm is orders of magnitude faster that the graphlet kernel for the same, or better, accuracy.