Supervised learning of analysis-sparsity priors with automatic differentiation
Paper and Code
Dec 15, 2021
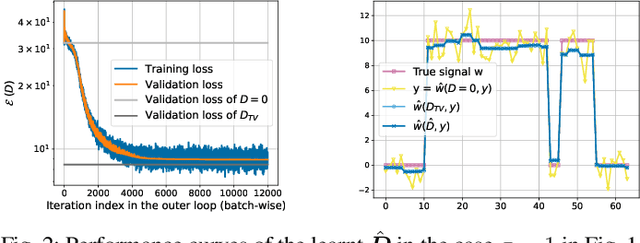
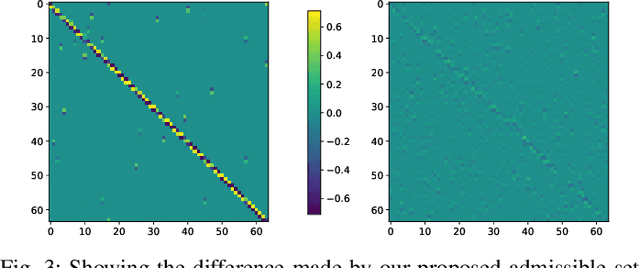
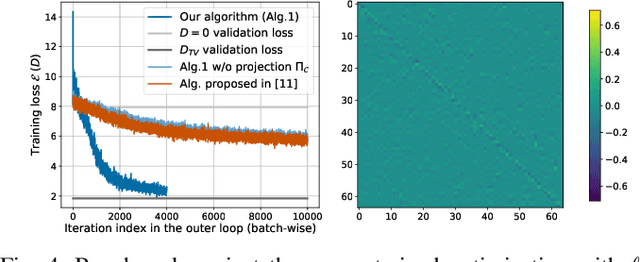
Sparsity priors are commonly used in denoising and image reconstruction. For analysis-type priors, a dictionary defines a representation of signals that is likely to be sparse. In most situations, this dictionary is not known, and is to be recovered from pairs of ground-truth signals and measurements, by minimizing the reconstruction error. This defines a hierarchical optimization problem, which can be cast as a bi-level optimization. Yet, this problem is unsolvable, as reconstructions and their derivative wrt the dictionary have no closed-form expression. However, reconstructions can be iteratively computed using the Forward-Backward splitting (FB) algorithm. In this paper, we approximate reconstructions by the output of the aforementioned FB algorithm. Then, we leverage automatic differentiation to evaluate the gradient of this output wrt the dictionary, which we learn with projected gradient descent. Experiments show that our algorithm successfully learns the 1D Total Variation (TV) dictionary from piecewise constant signals. For the same case study, we propose to constrain our search to dictionaries of 0-centered columns, which removes undesired local minima and improves numerical stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge