Scaling Law for Stochastic Gradient Descent in Quadratically Parameterized Linear Regression

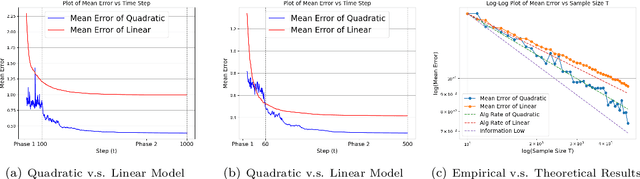
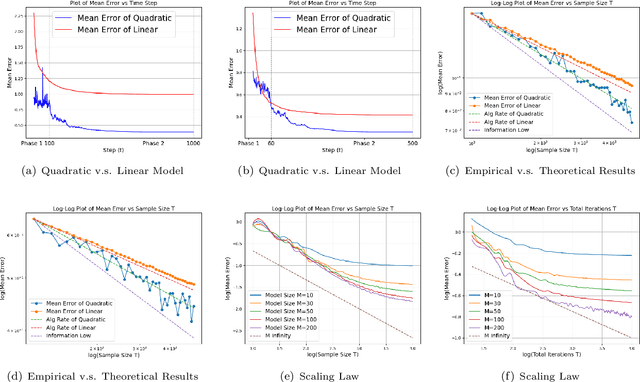
In machine learning, the scaling law describes how the model performance improves with the model and data size scaling up. From a learning theory perspective, this class of results establishes upper and lower generalization bounds for a specific learning algorithm. Here, the exact algorithm running using a specific model parameterization often offers a crucial implicit regularization effect, leading to good generalization. To characterize the scaling law, previous theoretical studies mainly focus on linear models, whereas, feature learning, a notable process that contributes to the remarkable empirical success of neural networks, is regretfully vacant. This paper studies the scaling law over a linear regression with the model being quadratically parameterized. We consider infinitely dimensional data and slope ground truth, both signals exhibiting certain power-law decay rates. We study convergence rates for Stochastic Gradient Descent and demonstrate the learning rates for variables will automatically adapt to the ground truth. As a result, in the canonical linear regression, we provide explicit separations for generalization curves between SGD with and without feature learning, and the information-theoretical lower bound that is agnostic to parametrization method and the algorithm. Our analysis for decaying ground truth provides a new characterization for the learning dynamic of the model.

Accelerated Gradient Algorithms with Adaptive Subspace Search for Instance-Faster Optimization

Gradient-based minimax optimal algorithms have greatly promoted the development of continuous optimization and machine learning. One seminal work due to Yurii Nesterov [Nes83a] established $\tilde{\mathcal{O}}(\sqrt{L/\mu})$ gradient complexity for minimizing an $L$-smooth $\mu$-strongly convex objective. However, an ideal algorithm would adapt to the explicit complexity of a particular objective function and incur faster rates for simpler problems, triggering our reconsideration of two defeats of existing optimization modeling and analysis. (i) The worst-case optimality is neither the instance optimality nor such one in reality. (ii) Traditional $L$-smoothness condition may not be the primary abstraction/characterization for modern practical problems. In this paper, we open up a new way to design and analyze gradient-based algorithms with direct applications in machine learning, including linear regression and beyond. We introduce two factors $(\alpha, \tau_{\alpha})$ to refine the description of the degenerated condition of the optimization problems based on the observation that the singular values of Hessian often drop sharply. We design adaptive algorithms that solve simpler problems without pre-known knowledge with reduced gradient or analogous oracle accesses. The algorithms also improve the state-of-art complexities for several problems in machine learning, thereby solving the open problem of how to design faster algorithms in light of the known complexity lower bounds. Specially, with the $\mathcal{O}(1)$-nuclear norm bounded, we achieve an optimal $\tilde{\mathcal{O}}(\mu^{-1/3})$ (v.s. $\tilde{\mathcal{O}}(\mu^{-1/2})$) gradient complexity for linear regression. We hope this work could invoke the rethinking for understanding the difficulty of modern problems in optimization.

CORE: Common Random Reconstruction for Distributed Optimization with Provable Low Communication Complexity

With distributed machine learning being a prominent technique for large-scale machine learning tasks, communication complexity has become a major bottleneck for speeding up training and scaling up machine numbers. In this paper, we propose a new technique named Common randOm REconstruction(CORE), which can be used to compress the information transmitted between machines in order to reduce communication complexity without other strict conditions. Especially, our technique CORE projects the vector-valued information to a low-dimensional one through common random vectors and reconstructs the information with the same random noises after communication. We apply CORE to two distributed tasks, respectively convex optimization on linear models and generic non-convex optimization, and design new distributed algorithms, which achieve provably lower communication complexities. For example, we show for linear models CORE-based algorithm can encode the gradient vector to $\mathcal{O}(1)$-bits (against $\mathcal{O}(d)$), with the convergence rate not worse, preceding the existing results.