Scaling Law for Stochastic Gradient Descent in Quadratically Parameterized Linear Regression
Paper and Code
Feb 13, 2025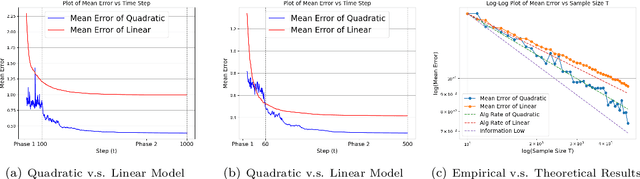
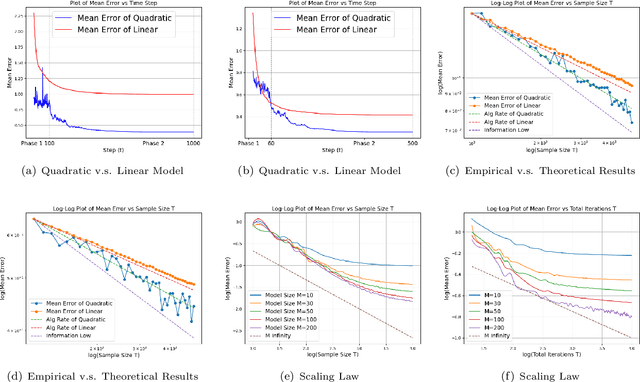
In machine learning, the scaling law describes how the model performance improves with the model and data size scaling up. From a learning theory perspective, this class of results establishes upper and lower generalization bounds for a specific learning algorithm. Here, the exact algorithm running using a specific model parameterization often offers a crucial implicit regularization effect, leading to good generalization. To characterize the scaling law, previous theoretical studies mainly focus on linear models, whereas, feature learning, a notable process that contributes to the remarkable empirical success of neural networks, is regretfully vacant. This paper studies the scaling law over a linear regression with the model being quadratically parameterized. We consider infinitely dimensional data and slope ground truth, both signals exhibiting certain power-law decay rates. We study convergence rates for Stochastic Gradient Descent and demonstrate the learning rates for variables will automatically adapt to the ground truth. As a result, in the canonical linear regression, we provide explicit separations for generalization curves between SGD with and without feature learning, and the information-theoretical lower bound that is agnostic to parametrization method and the algorithm. Our analysis for decaying ground truth provides a new characterization for the learning dynamic of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge