Hyperplane Arrangements and Fixed Points in Iterated PWL Neural Networks

We leverage the framework of hyperplane arrangements to analyze potential regions of (stable) fixed points. We provide an upper bound on the number of fixed points for multi-layer neural networks equipped with piecewise linear (PWL) activation functions with arbitrary many linear pieces. The theoretical optimality of the exponential growth in the number of layers of the latter bound is shown. Specifically, we also derive a sharper upper bound on the number of stable fixed points for one-hidden-layer networks with hard tanh activation.

Expressiveness of Neural Networks Having Width Equal or Below the Input Dimension

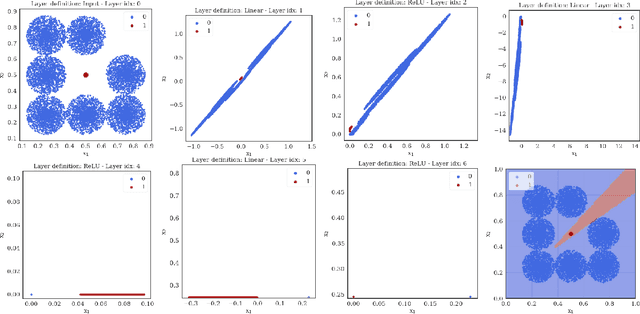
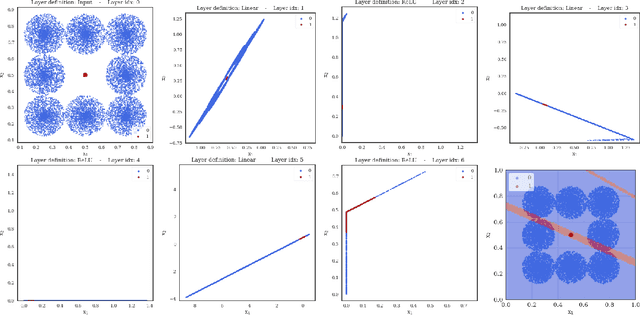
The expressiveness of deep neural networks of bounded width has recently been investigated in a series of articles. The understanding about the minimum width needed to ensure universal approximation for different kind of activation functions has progressively been extended (Park et al., 2020). In particular, it turned out that, with respect to approximation on general compact sets in the input space, a network width less than or equal to the input dimension excludes universal approximation. In this work, we focus on network functions of width less than or equal to the latter critical bound. We prove that in this regime the exact fit of partially constant functions on disjoint compact sets is still possible for ReLU network functions under some conditions on the mutual location of these components. Conversely, we conclude from a maximum principle that for all continuous and monotonic activation functions, universal approximation of arbitrary continuous functions is impossible on sets that coincide with the boundary of an open set plus an inner point of that set. We also show that some network functions of maximum width two, respectively one, allow universal approximation on finite sets.

A Hybrid Objective Function for Robustness of Artificial Neural Networks -- Estimation of Parameters in a Mechanical System

In several studies, hybrid neural networks have proven to be more robust against noisy input data compared to plain data driven neural networks. We consider the task of estimating parameters of a mechanical vehicle model based on acceleration profiles. We introduce a convolutional neural network architecture that is capable to predict the parameters for a family of vehicle models that differ in the unknown parameters. We introduce a convolutional neural network architecture that given sequential data predicts the parameters of the underlying data's dynamics. This network is trained with two objective functions. The first one constitutes a more naive approach that assumes that the true parameters are known. The second objective incorporates the knowledge of the underlying dynamics and is therefore considered as hybrid approach. We show that in terms of robustness, the latter outperforms the first objective on noisy input data.

SVIRO: Synthetic Vehicle Interior Rear Seat Occupancy Dataset and Benchmark

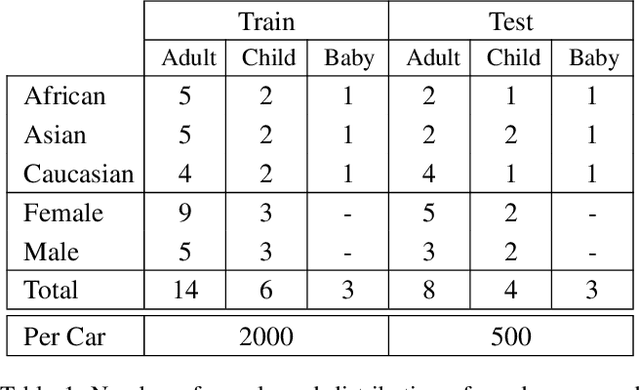
We release SVIRO, a synthetic dataset for sceneries in the passenger compartment of ten different vehicles, in order to analyze machine learning-based approaches for their generalization capacities and reliability when trained on a limited number of variations (e.g. identical backgrounds and textures, few instances per class). This is in contrast to the intrinsically high variability of common benchmark datasets, which focus on improving the state-of-the-art of general tasks. Our dataset contains bounding boxes for object detection, instance segmentation masks, keypoints for pose estimation and depth images for each synthetic scenery as well as images for each individual seat for classification. The advantage of our use-case is twofold: The proximity to a realistic application to benchmark new approaches under novel circumstances while reducing the complexity to a more tractable environment, such that applications and theoretical questions can be tested on a more challenging dataset as toy problems. The data and evaluation server are available under https://sviro.kl.dfki.de.

On decision regions of narrow deep neural networks

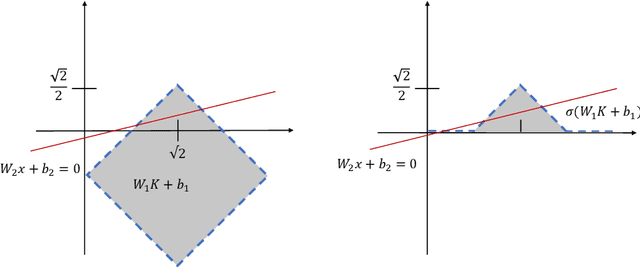
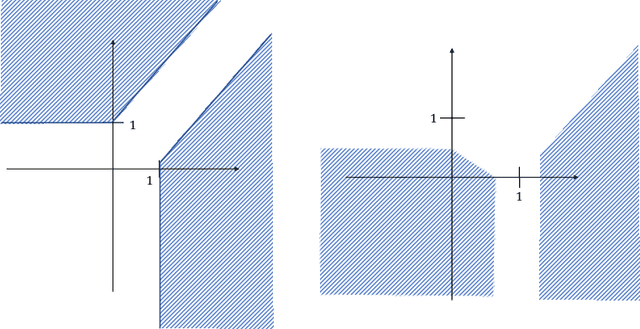
We show that for neural network functions that have width less or equal to the input dimension all connected components of decision regions are unbounded. The result holds for continuous and strictly monotonic activation functions as well as for ReLU activation. This complements recent results on approximation capabilities of [Hanin 2017 Approximating] and connectivity of decision regions of [Nguyen 2018 Neural] for such narrow neural networks. Further, we give an example that negatively answers the question posed in [Nguyen 2018 Neural] whether one of their main results still holds for ReLU activation. Our results are illustrated by means of numerical experiments.