Expressiveness of Neural Networks Having Width Equal or Below the Input Dimension

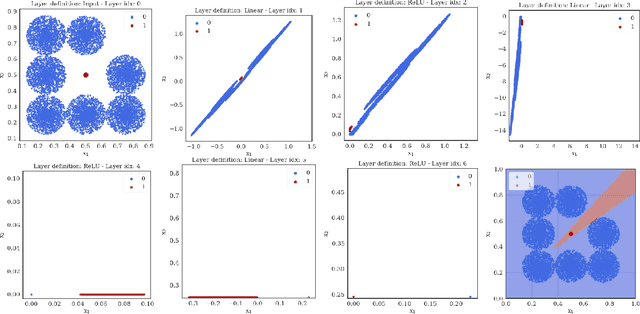
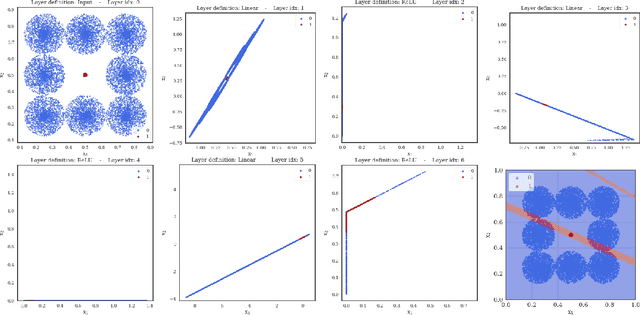
The expressiveness of deep neural networks of bounded width has recently been investigated in a series of articles. The understanding about the minimum width needed to ensure universal approximation for different kind of activation functions has progressively been extended (Park et al., 2020). In particular, it turned out that, with respect to approximation on general compact sets in the input space, a network width less than or equal to the input dimension excludes universal approximation. In this work, we focus on network functions of width less than or equal to the latter critical bound. We prove that in this regime the exact fit of partially constant functions on disjoint compact sets is still possible for ReLU network functions under some conditions on the mutual location of these components. Conversely, we conclude from a maximum principle that for all continuous and monotonic activation functions, universal approximation of arbitrary continuous functions is impossible on sets that coincide with the boundary of an open set plus an inner point of that set. We also show that some network functions of maximum width two, respectively one, allow universal approximation on finite sets.