On decision regions of narrow deep neural networks

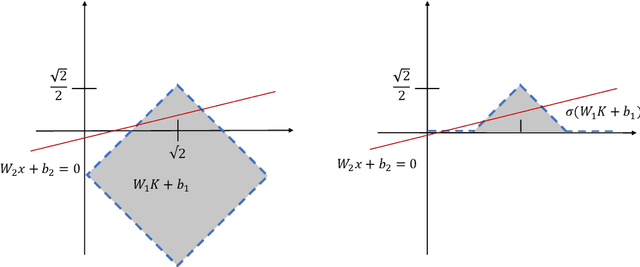
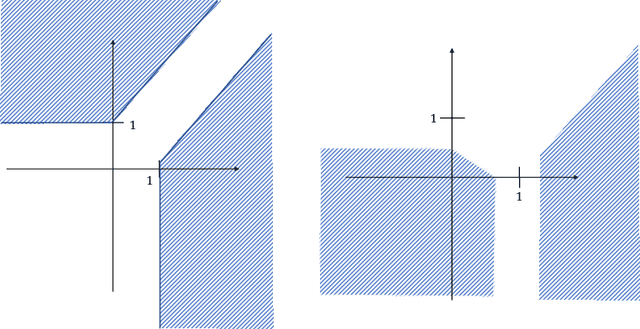
We show that for neural network functions that have width less or equal to the input dimension all connected components of decision regions are unbounded. The result holds for continuous and strictly monotonic activation functions as well as for ReLU activation. This complements recent results on approximation capabilities of [Hanin 2017 Approximating] and connectivity of decision regions of [Nguyen 2018 Neural] for such narrow neural networks. Further, we give an example that negatively answers the question posed in [Nguyen 2018 Neural] whether one of their main results still holds for ReLU activation. Our results are illustrated by means of numerical experiments.