SPOCK 2.0: Update to the FeatureClassifier in the Stability of Planetary Orbital Configurations Klassifier

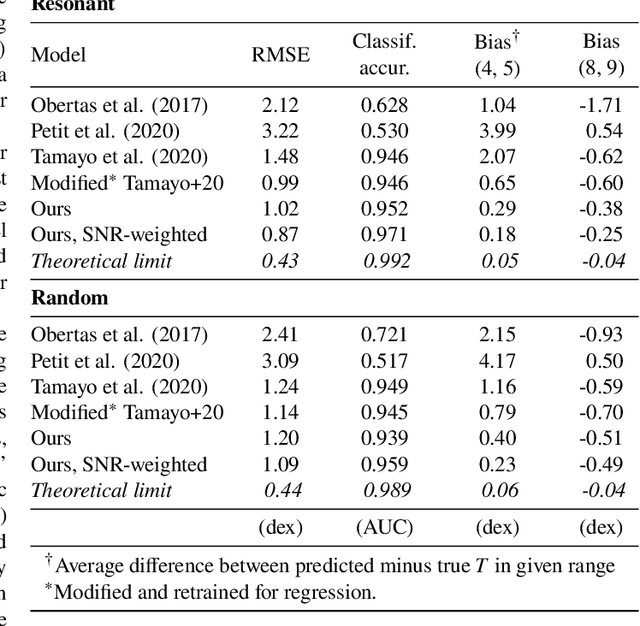
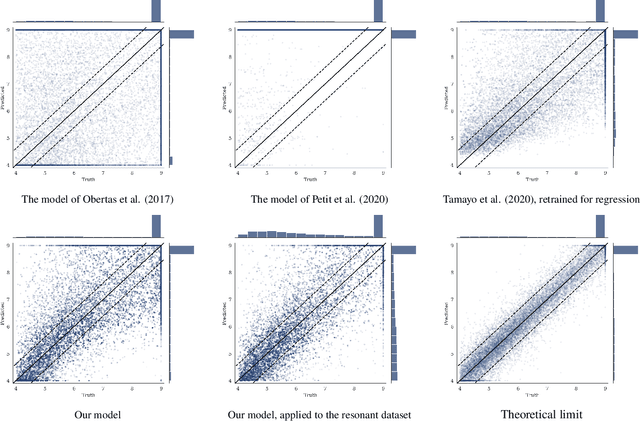
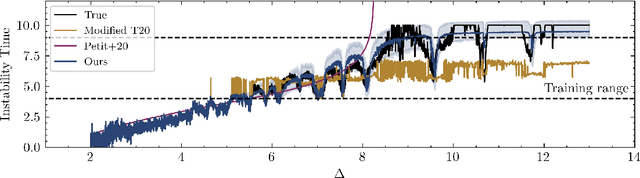
The Stability of Planetary Orbital Configurations Klassifier (SPOCK) package collects machine learning models for predicting the stability and collisional evolution of compact planetary systems. In this paper we explore improvements to SPOCK's binary stability classifier (FeatureClassifier), which predicts orbital stability by collecting data over a short N-body integration of a system. We find that by using a system-specific timescale (rather than a fixed $10^4$ orbits) for the integration, and by using this timescale as an additional feature, we modestly improve the model's AUC metric from 0.943 to 0.950 (AUC=1 for a perfect model). We additionally discovered that $\approx 10\%$ of N-body integrations in SPOCK's original training dataset were duplicated by accident, and that $<1\%$ were misclassified as stable when they in fact led to ejections. We provide a cleaned dataset of 100,000+ unique integrations, release a newly trained stability classification model, and make minor updates to the API.

A Bayesian neural network predicts the dissolution of compact planetary systems

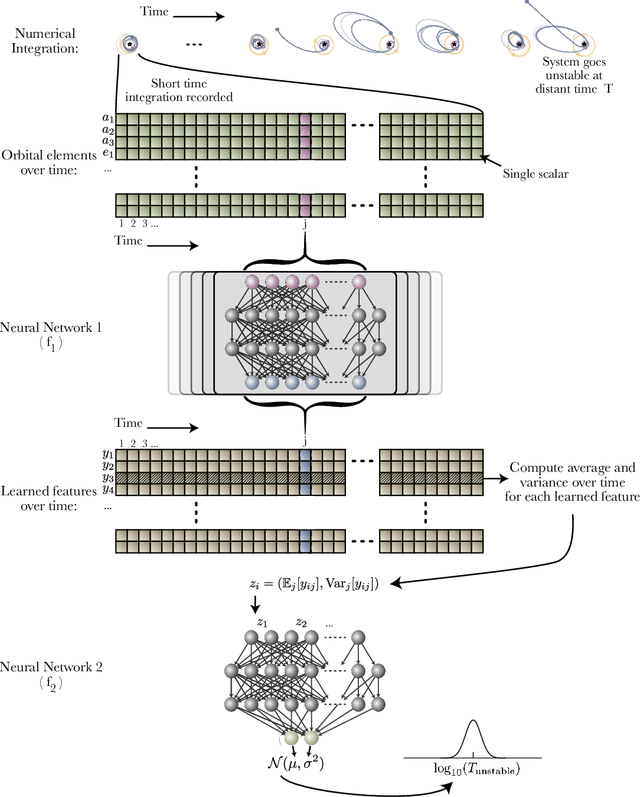
Despite over three hundred years of effort, no solutions exist for predicting when a general planetary configuration will become unstable. We introduce a deep learning architecture to push forward this problem for compact systems. While current machine learning algorithms in this area rely on scientist-derived instability metrics, our new technique learns its own metrics from scratch, enabled by a novel internal structure inspired from dynamics theory. Our Bayesian neural network model can accurately predict not only if, but also when a compact planetary system with three or more planets will go unstable. Our model, trained directly from short N-body time series of raw orbital elements, is more than two orders of magnitude more accurate at predicting instability times than analytical estimators, while also reducing the bias of existing machine learning algorithms by nearly a factor of three. Despite being trained on compact resonant and near-resonant three-planet configurations, the model demonstrates robust generalization to both non-resonant and higher multiplicity configurations, in the latter case outperforming models fit to that specific set of integrations. The model computes instability estimates up to five orders of magnitude faster than a numerical integrator, and unlike previous efforts provides confidence intervals on its predictions. Our inference model is publicly available in the SPOCK package, with training code open-sourced.