Defining error accumulation in ML atmospheric simulators

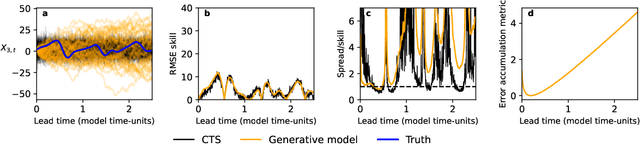
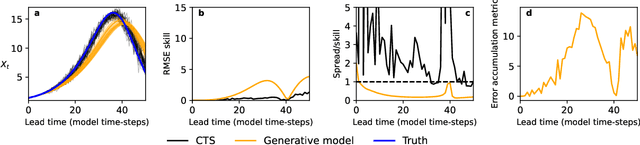
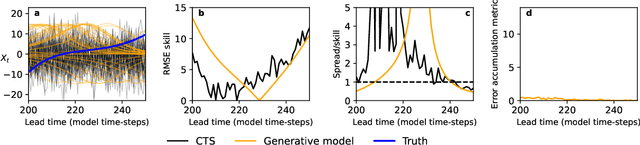
Machine learning (ML) has recently shown significant promise in modelling atmospheric systems, such as the weather. Many of these ML models are autoregressive, and error accumulation in their forecasts is a key problem. However, there is no clear definition of what `error accumulation' actually entails. In this paper, we propose a definition and an associated metric to measure it. Our definition distinguishes between errors which are due to model deficiencies, which we may hope to fix, and those due to the intrinsic properties of atmospheric systems (chaos, unobserved variables), which are not fixable. We illustrate the usefulness of this definition by proposing a simple regularization loss penalty inspired by it. This approach shows performance improvements (according to RMSE and spread/skill) in a selection of atmospheric systems, including the real-world weather prediction task.

Machine Learning for Stochastic Parametrisation

Atmospheric models used for weather and climate prediction are traditionally formulated in a deterministic manner. In other words, given a particular state of the resolved scale variables, the most likely forcing from the sub-grid scale processes is estimated and used to predict the evolution of the large-scale flow. However, the lack of scale-separation in the atmosphere means that this approach is a large source of error in forecasts. Over recent years, an alternative paradigm has developed: the use of stochastic techniques to characterise uncertainty in small-scale processes. These techniques are now widely used across weather, sub-seasonal, seasonal, and climate timescales. In parallel, recent years have also seen significant progress in replacing parametrisation schemes using machine learning (ML). This has the potential to both speed up and improve our numerical models. However, the focus to date has largely been on deterministic approaches. In this position paper, we bring together these two key developments, and discuss the potential for data-driven approaches for stochastic parametrisation. We highlight early studies in this area, and draw attention to the novel challenges that remain.

Stochastic Parameterizations: Better Modelling of Temporal Correlations using Probabilistic Machine Learning

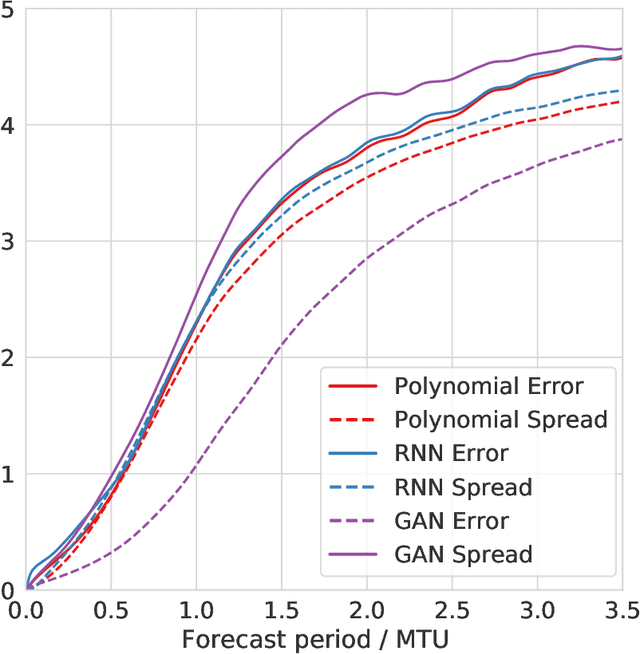
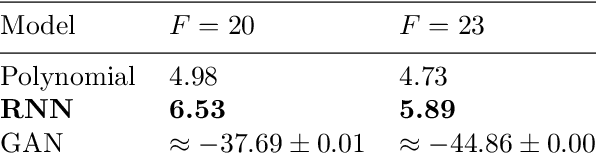
The modelling of small-scale processes is a major source of error in climate models, hindering the accuracy of low-cost models which must approximate such processes through parameterization. Using stochasticity and machine learning have led to better models but there is a lack of work on combining the benefits from both. We show that by using a physically-informed recurrent neural network within a probabilistic framework, our resulting model for the Lorenz 96 atmospheric simulation is competitive and often superior to both a bespoke baseline and an existing probabilistic machine-learning (GAN) one. This is due to a superior ability to model temporal correlations compared to standard first-order autoregressive schemes. The model also generalises to unseen regimes. We evaluate across a number of metrics from the literature, but also discuss how the probabilistic metric of likelihood may be a unifying choice for future probabilistic climate models.

Machine Learning for Stochastic Parameterization: Generative Adversarial Networks in the Lorenz '96 Model

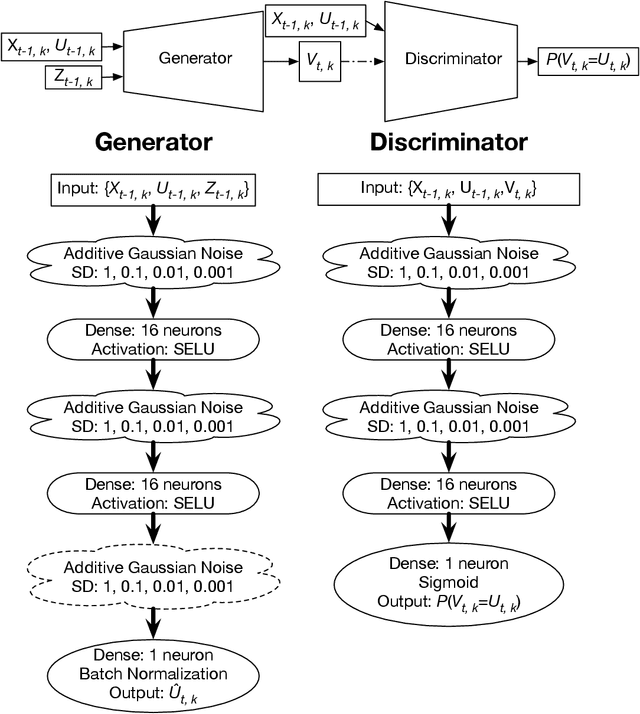
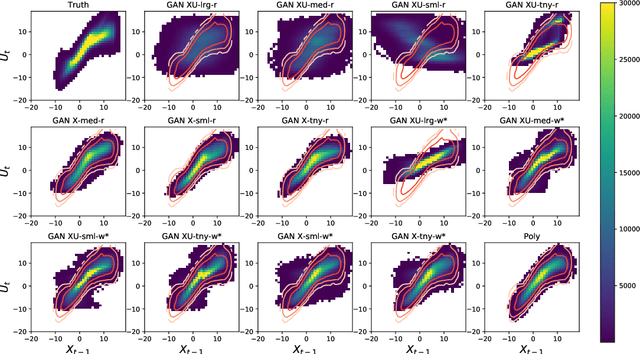
Stochastic parameterizations account for uncertainty in the representation of unresolved sub-grid processes by sampling from the distribution of possible sub-grid forcings. Some existing stochastic parameterizations utilize data-driven approaches to characterize uncertainty, but these approaches require significant structural assumptions that can limit their scalability. Machine learning models, including neural networks, are able to represent a wide range of distributions and build optimized mappings between a large number of inputs and sub-grid forcings. Recent research on machine learning parameterizations has focused only on deterministic parameterizations. In this study, we develop a stochastic parameterization using the generative adversarial network (GAN) machine learning framework. The GAN stochastic parameterization is trained and evaluated on output from the Lorenz '96 model, which is a common baseline model for evaluating both parameterization and data assimilation techniques. We evaluate different ways of characterizing the input noise for the model and perform model runs with the GAN parameterization at weather and climate timescales. Some of the GAN configurations perform better than a baseline bespoke parameterization at both timescales, and the networks closely reproduce the spatio-temporal correlations and regimes of the Lorenz '96 system. We also find that in general those models which produce skillful forecasts are also associated with the best climate simulations.