Defining error accumulation in ML atmospheric simulators

Machine learning (ML) has recently shown significant promise in modelling atmospheric systems, such as the weather. Many of these ML models are autoregressive, and error accumulation in their forecasts is a key problem. However, there is no clear definition of what `error accumulation' actually entails. In this paper, we propose a definition and an associated metric to measure it. Our definition distinguishes between errors which are due to model deficiencies, which we may hope to fix, and those due to the intrinsic properties of atmospheric systems (chaos, unobserved variables), which are not fixable. We illustrate the usefulness of this definition by proposing a simple regularization loss penalty inspired by it. This approach shows performance improvements (according to RMSE and spread/skill) in a selection of atmospheric systems, including the real-world weather prediction task.

A Temporal Bias Correction using a Machine Learning Attention model

Climate models are biased with respect to real world observations and usually need to be calibrated prior to impact studies. The suite of statistical methods that enable such calibrations is called bias correction (BC). However, current BC methods struggle to adjust for temporal biases, because they disregard the dependence between consecutive time-points. As a result, climate statistics with long-range temporal properties, such as heatwave duration and frequency, cannot be corrected accurately, making it more difficult to produce reliable impact studies on such climate statistics. In this paper, we offer a novel BC methodology to correct for temporal biases. This is made possible by i) re-thinking BC as a probability model rather than an algorithmic procedure, and ii) adapting state-of-the-art machine-learning (ML) probabilistic attention models to fit the BC task. With a case study of heatwave duration statistics in Abuja, Nigeria, and Tokyo, Japan, we show striking results compared to current climate model outputs and alternative BC methods.

Taylorformer: Probabilistic Predictions for Time Series and other Processes

We propose the Taylorformer for time series and other random processes. Its two key components are: 1) the LocalTaylor wrapper to learn how and when to use Taylor series-based approximations for predictions, and 2) the MHA-X attention block which makes predictions in a way inspired by how Gaussian Processes' mean predictions are linear smoothings of contextual data. Taylorformer outperforms the state-of-the-art on several forecasting datasets, including electricity, oil temperatures and exchange rates with at least 14% improvement in MSE on all tasks, and better likelihood on 5/6 classic Neural Process tasks such as meta-learning 1D functions. Taylorformer combines desirable features from the Neural Process (uncertainty-aware predictions and consistency) and forecasting (predictive accuracy) literature, two previously distinct bodies.

Don't Waste Data: Transfer Learning to Leverage All Data for Machine-Learnt Climate Model Emulation

How can we learn from all available data when training machine-learnt climate models, without incurring any extra cost at simulation time? Typically, the training data comprises coarse-grained high-resolution data. But only keeping this coarse-grained data means the rest of the high-resolution data is thrown out. We use a transfer learning approach, which can be applied to a range of machine learning models, to leverage all the high-resolution data. We use three chaotic systems to show it stabilises training, gives improved generalisation performance and results in better forecasting skill. Our anonymised code is at https://www.dropbox.com/sh/0o1pks1i90mix3q/AAAMGfyD7EyOkdnA_Hp5ZpiWa?dl=0

Stochastic Parameterizations: Better Modelling of Temporal Correlations using Probabilistic Machine Learning

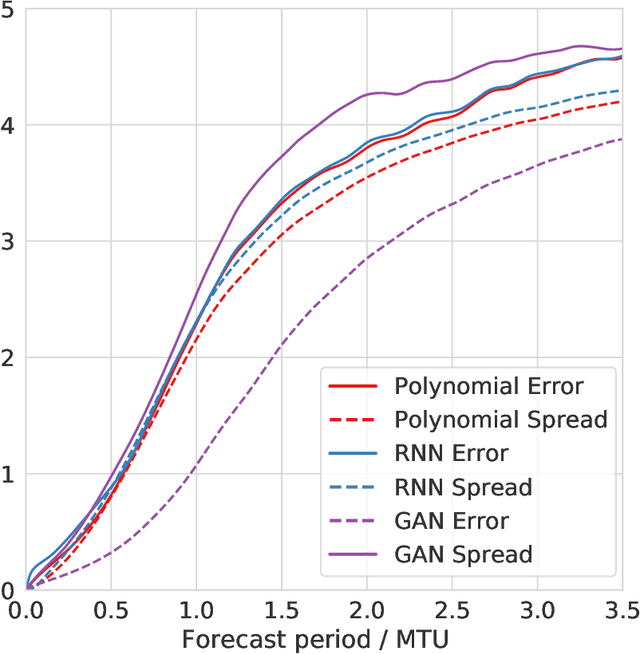
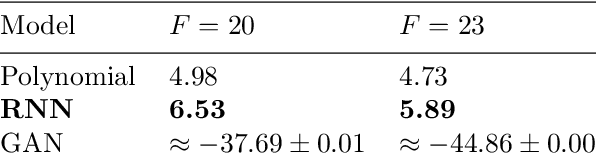
The modelling of small-scale processes is a major source of error in climate models, hindering the accuracy of low-cost models which must approximate such processes through parameterization. Using stochasticity and machine learning have led to better models but there is a lack of work on combining the benefits from both. We show that by using a physically-informed recurrent neural network within a probabilistic framework, our resulting model for the Lorenz 96 atmospheric simulation is competitive and often superior to both a bespoke baseline and an existing probabilistic machine-learning (GAN) one. This is due to a superior ability to model temporal correlations compared to standard first-order autoregressive schemes. The model also generalises to unseen regimes. We evaluate across a number of metrics from the literature, but also discuss how the probabilistic metric of likelihood may be a unifying choice for future probabilistic climate models.