An adaptive shortest-solution guided decimation approach to sparse high-dimensional linear regression

High-dimensional linear regression model is the most popular statistical model for high-dimensional data, but it is quite a challenging task to achieve a sparse set of regression coefficients. In this paper, we propose a simple heuristic algorithm to construct sparse high-dimensional linear regression models, which is adapted from the shortest solution-guided decimation algorithm and is referred to as ASSD. This algorithm constructs the support of regression coefficients under the guidance of the least-squares solution of the recursively decimated linear equations, and it applies an early-stopping criterion and a second-stage thresholding procedure to refine this support. Our extensive numerical results demonstrate that ASSD outperforms LASSO, vector approximate message passing, and two other representative greedy algorithms in solution accuracy and robustness. ASSD is especially suitable for linear regression problems with highly correlated measurement matrices encountered in real-world applications.

Learning by random walks in the weight space of the Ising perceptron

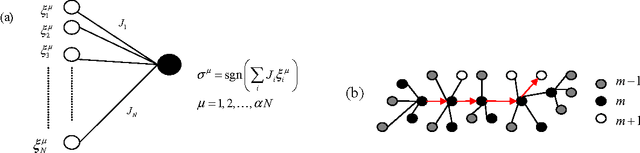
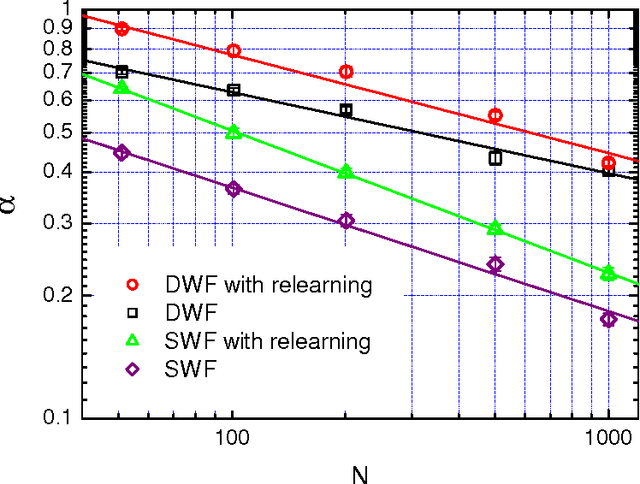
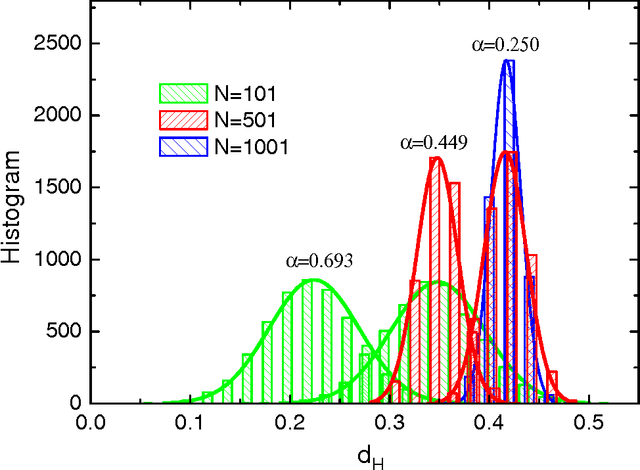
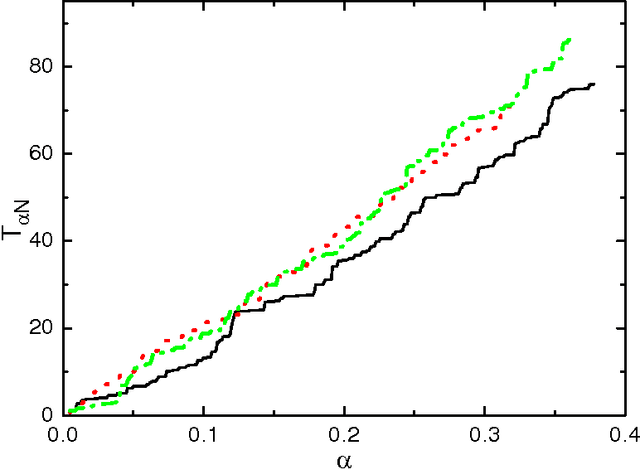
Several variants of a stochastic local search process for constructing the synaptic weights of an Ising perceptron are studied. In this process, binary patterns are sequentially presented to the Ising perceptron and are then learned as the synaptic weight configuration is modified through a chain of single- or double-weight flips within the compatible weight configuration space of the earlier learned patterns. This process is able to reach a storage capacity of $\alpha \approx 0.63$ for pattern length N = 101 and $\alpha \approx 0.41$ for N = 1001. If in addition a relearning process is exploited, the learning performance is further improved to a storage capacity of $\alpha \approx 0.80$ for N = 101 and $\alpha \approx 0.42$ for N=1001. We found that, for a given learning task, the solutions constructed by the random walk learning process are separated by a typical Hamming distance, which decreases with the constraint density $\alpha$ of the learning task; at a fixed value of $\alpha$, the width of the Hamming distance distributions decreases with $N$.