Learning by random walks in the weight space of the Ising perceptron
Paper and Code
May 30, 2010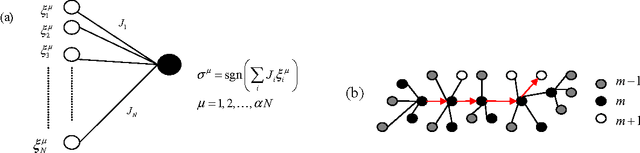
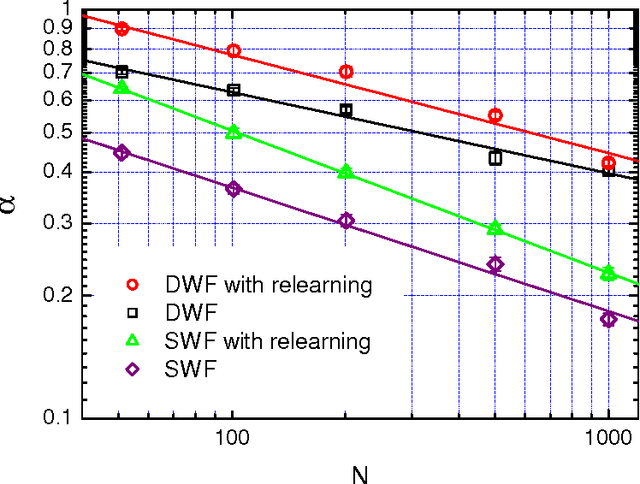
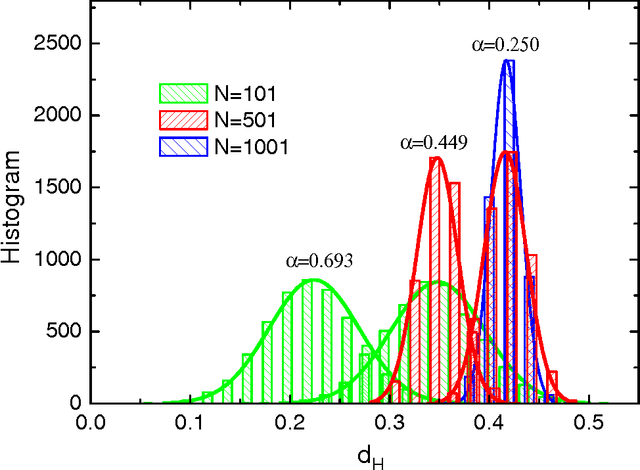
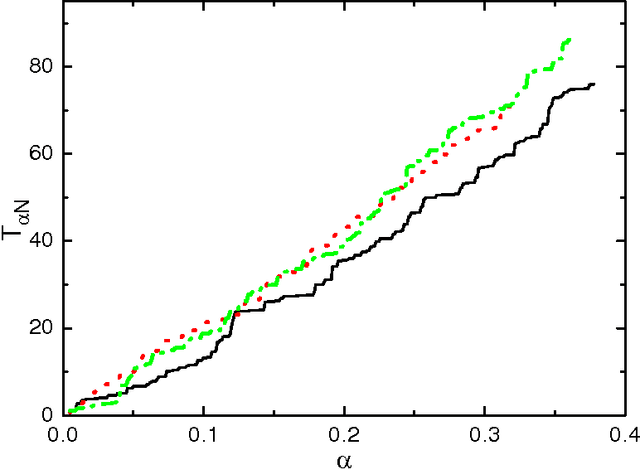
Several variants of a stochastic local search process for constructing the synaptic weights of an Ising perceptron are studied. In this process, binary patterns are sequentially presented to the Ising perceptron and are then learned as the synaptic weight configuration is modified through a chain of single- or double-weight flips within the compatible weight configuration space of the earlier learned patterns. This process is able to reach a storage capacity of $\alpha \approx 0.63$ for pattern length N = 101 and $\alpha \approx 0.41$ for N = 1001. If in addition a relearning process is exploited, the learning performance is further improved to a storage capacity of $\alpha \approx 0.80$ for N = 101 and $\alpha \approx 0.42$ for N=1001. We found that, for a given learning task, the solutions constructed by the random walk learning process are separated by a typical Hamming distance, which decreases with the constraint density $\alpha$ of the learning task; at a fixed value of $\alpha$, the width of the Hamming distance distributions decreases with $N$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge