Plant Species Recognition with Optimized 3D Polynomial Neural Networks and Variably Overlapping Time-Coherent Sliding Window

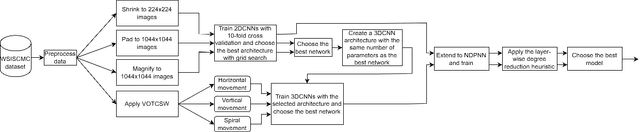
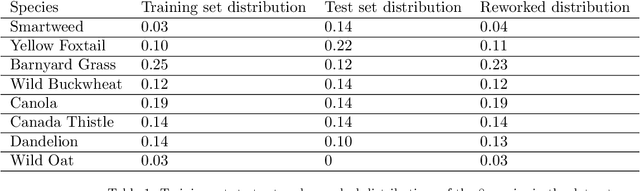
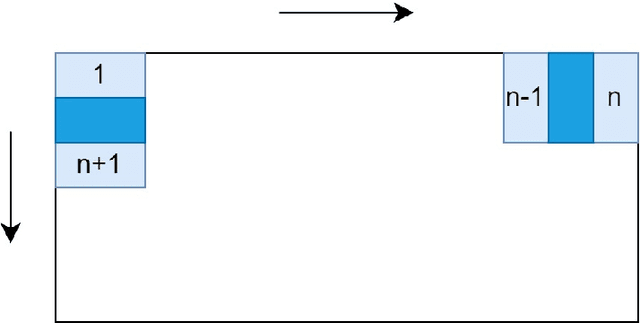
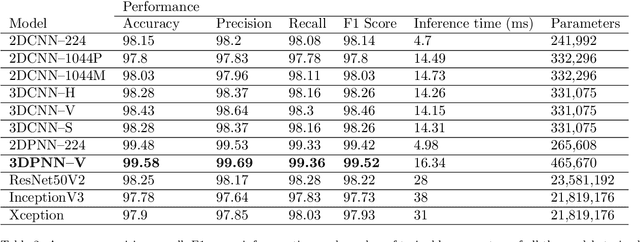
Recently, the EAGL-I system was developed to rapidly create massive labeled datasets of plants intended to be commonly used by farmers and researchers to create AI-driven solutions in agriculture. As a result, a publicly available plant species recognition dataset composed of 40,000 images with different sizes consisting of 8 plant species was created with the system in order to demonstrate its capabilities. This paper proposes a novel method, called Variably Overlapping Time-Coherent Sliding Window (VOTCSW), that transforms a dataset composed of images with variable size to a 3D representation with fixed size that is suitable for convolutional neural networks, and demonstrates that this representation is more informative than resizing the images of the dataset to a given size. We theoretically formalized the use cases of the method as well as its inherent properties and we proved that it has an oversampling and a regularization effect on the data. By combining the VOTCSW method with the 3D extension of a recently proposed machine learning model called 1-Dimensional Polynomial Neural Networks, we were able to create a model that achieved a state-of-the-art accuracy of 99.9% on the dataset created by the EAGL-I system, surpassing well-known architectures such as ResNet and Inception. In addition, we created a heuristic algorithm that enables the degree reduction of any pre-trained N-Dimensional Polynomial Neural Network and which compresses it without altering its performance, thus making the model faster and lighter. Furthermore, we established that the currently available dataset could not be used for machine learning in its present form, due to a substantial class imbalance between the training set and the test set. Hence, we created a specific preprocessing and a model development framework that enabled us to improve the accuracy from 49.23% to 99.9%.

1-Dimensional polynomial neural networks for audio signal related problems

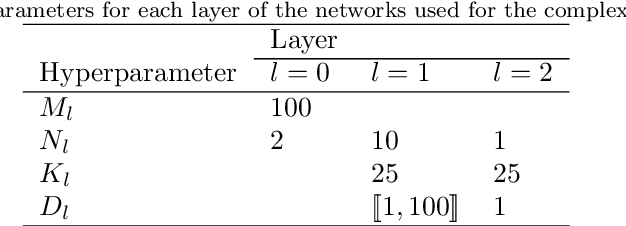
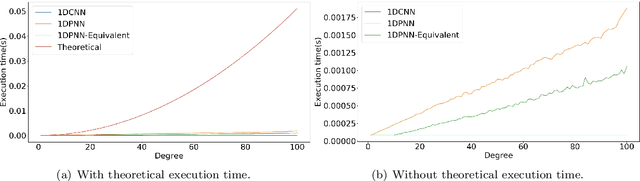
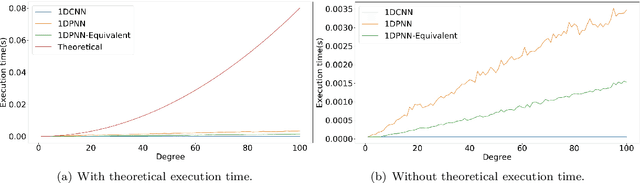
In addition to being extremely non-linear, modern problems require millions if not billions of parameters to solve or at least to get a good approximation of the solution, and neural networks are known to assimilate that complexity by deepening and widening their topology in order to increase the level of non-linearity needed for a better approximation. However, compact topologies are always preferred to deeper ones as they offer the advantage of using less computational units and less parameters. This compacity comes at the price of reduced non-linearity and thus, of limited solution search space. We propose the 1-Dimensional Polynomial Neural Network (1DPNN) model that uses automatic polynomial kernel estimation for 1-Dimensional Convolutional Neural Networks (1DCNNs) and that introduces a high degree of non-linearity from the first layer which can compensate the need for deep and/or wide topologies. We show that this non-linearity introduces more computational complexity but enables the model to yield better results than a regular 1DCNN that has the same number of training parameters on various classification and regression problems related to audio signals. The experiments were conducted on three publicly available datasets and demonstrate that the proposed model can achieve a much faster convergence than a 1DCNN on the tackled regression problems.

Exploiting Heterogeneity in Operational Neural Networks by Synaptic Plasticity

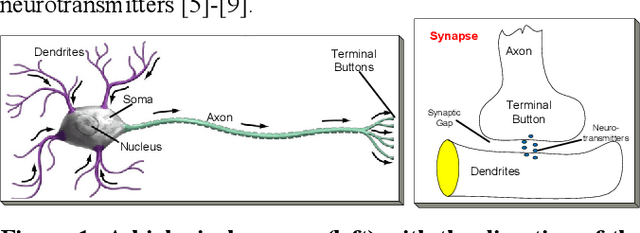
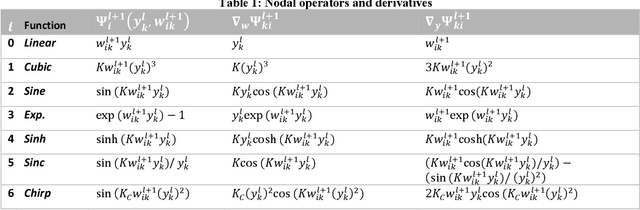
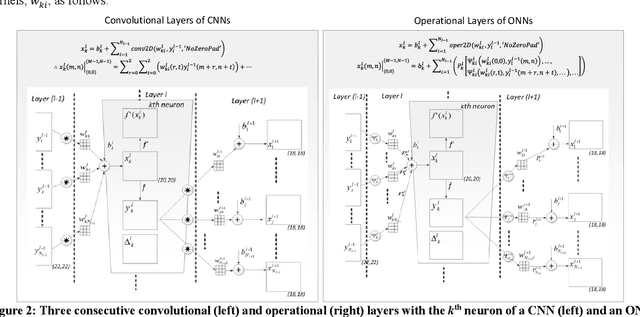
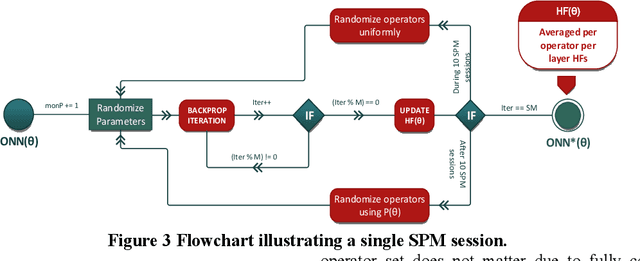
The recently proposed network model, Operational Neural Networks (ONNs), can generalize the conventional Convolutional Neural Networks (CNNs) that are homogenous only with a linear neuron model. As a heterogenous network model, ONNs are based on a generalized neuron model that can encapsulate any set of non-linear operators to boost diversity and to learn highly complex and multi-modal functions or spaces with minimal network complexity and training data. However, the default search method to find optimal operators in ONNs, the so-called Greedy Iterative Search (GIS) method, usually takes several training sessions to find a single operator set per layer. This is not only computationally demanding, also the network heterogeneity is limited since the same set of operators will then be used for all neurons in each layer. To address this deficiency and exploit a superior level of heterogeneity, in this study the focus is drawn on searching the best-possible operator set(s) for the hidden neurons of the network based on the Synaptic Plasticity paradigm that poses the essential learning theory in biological neurons. During training, each operator set in the library can be evaluated by their synaptic plasticity level, ranked from the worst to the best, and an elite ONN can then be configured using the top ranked operator sets found at each hidden layer. Experimental results over highly challenging problems demonstrate that the elite ONNs even with few neurons and layers can achieve a superior learning performance than GIS-based ONNs and as a result the performance gap over the CNNs further widens.

Self-Organized Operational Neural Networks with Generative Neurons

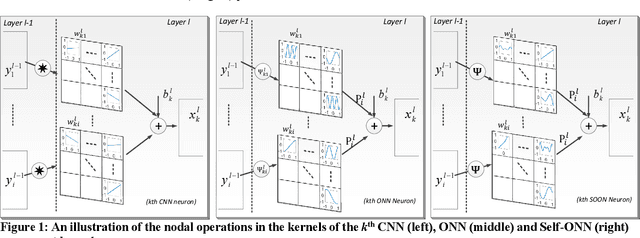
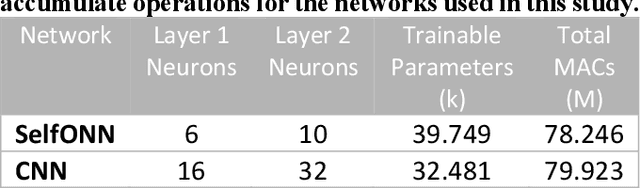
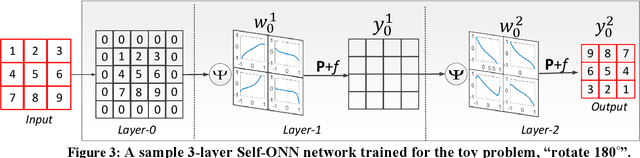
Operational Neural Networks (ONNs) have recently been proposed to address the well-known limitations and drawbacks of conventional Convolutional Neural Networks (CNNs) such as network homogeneity with the sole linear neuron model. ONNs are heterogenous networks with a generalized neuron model that can encapsulate any set of non-linear operators to boost diversity and to learn highly complex and multi-modal functions or spaces with minimal network complexity and training data. However, Greedy Iterative Search (GIS) method, which is the search method used to find optimal operators in ONNs takes many training sessions to find a single operator set per layer. This is not only computationally demanding, but the network heterogeneity is also limited since the same set of operators will then be used for all neurons in each layer. Moreover, the performance of ONNs directly depends on the operator set library used, which introduces a certain risk of performance degradation especially when the optimal operator set required for a particular task is missing from the library. In order to address these issues and achieve an ultimate heterogeneity level to boost the network diversity along with computational efficiency, in this study we propose Self-organized ONNs (Self-ONNs) with generative neurons that have the ability to adapt (optimize) the nodal operator of each connection during the training process. Therefore, Self-ONNs can have an utmost heterogeneity level required by the learning problem at hand. Moreover, this ability voids the need of having a fixed operator set library and the prior operator search within the library in order to find the best possible set of operators. We further formulate the training method to back-propagate the error through the operational layers of Self-ONNs.